Работа с файлами, построение графиков
Содержание
Базовая работа с файлами
Работа с файлом является работой с потоком. Как программист, вы можете представить, что находитесь на определённой позиции в потоке, а выполняемые вами операции ведутся относительно этой позиции.
Для того, чтобы начать работать с файлом, его необходимо открыть на чтение или запись. При этом Python предоставляет два режима работы на выбор: текстовый и байтовый. В основе текстового режима лежат символы - файл представляется, как поток текстовых символов (по умолчанию в кодировке Unicode). В основе байтового режима обрабатываемая единица потока - байт.
Чтение
Пусть в рабочей директории находится файл hello.txt, содержащий всего две строки:
Я первая строка файла! А я вторая!
Для открытия файла используется функция open.
>>> file = open('hello.txt')
>>> file
<_io.TextIOWrapper name='hello.txt' mode='r' encoding='UTF-8'>
Её первый аргумент - путь до файла.
Помимо имени можно указать режим работы mode, по умолчанию это чтение в текстовом режиме.
Открытый на чтение файл можно
- прочитать полностью
file.read() - прочитать
sizeсимволовfile.read(size) - прочитать строку
file.readline() - прочитать все строки
file.readlines()
После завершения работы с файлом, его необходимо закрыть file.close().
Вот как выглядит результат работы этих операций:
>>> file.readline()
'Я первая строка файла!\n'
>>> file.read(2)
'А '
>>> file.read(3)
'я в'
>>> file.read(100)
'торая!\n'
>>> file.read(1)
''
>>> file.close()
Заметьте, что file.read(2) считал символы со втрой строки файла, поскольку первая операция file.readline() перенесла поток в новую позицию (на вторую строку).
Также, после file.read(100) мы передвинулись в конец потока, поэтому file.read(1) возвращает пустую строку.
Файл можно считывать построчно с помощью цикла for
>>> file = open('hello.txt')
>>> for line in file:
... print(repr(line))
...
'Я первая строка файла!\n'
'А я вторая!\n'
>>> file.close()
Здесь для печати специально использована функция repr(), чтобы показать, что в строку входит символ конца строки \n.
Очистить строку от него и других символов-пробелов можно с помощью str.strip().
Хорошей практикой является использование конструкции with
>>> with open('hello.txt') as file:
... for line in file:
... print(line.strip())
...
Я первая строка файла!
А я вторая!
В конце работы блока with файл автоматически закроется.
Запись
Для записи в файл необходимо выставить режим на запись
- 'w' - удаление всего содержимого, запись в начало
- 'a' - запись в конец (дописывание)
Типичные операции
file.write(str)- запись строкиfile.writelines(iterable)- запись нескольких строк, при этом разделитель строк нужно выставлять вручную
Пример записи трёх строк в файл out.txt с последующим выводом содержимого файла
>>> file = open('out.txt', 'w')
>>> file.write('AAA\n')
4
>>> file.writelines(['BBB\n', 'CCC\n'])
>>> file.close()
>>> file = open('out.txt')
>>> content = file.read()
>>> print(content)
AAA
BBB
CCC
>>> file.close()
Кроме того, можно производить запись в файл с помощью привычной функции print.
У неё есть параметр file для перенаправления вывода (по умолчанию это стандартный поток вывода stdout).
Измерение времени работы кода
Один из простых способов замерить время работы участка кода -- воспользоваться функцией time.time(), возвращающей системное время в секундах (см. Epoch time).
Вот пример работы:
>>> import time
>>> start = time.time() # начало замера
>>> print('Hello')
Hello
>>> end = time.time() # конец замера
>>> print(end-start)
10.43204402923584
Модуль numpy
Библиотека numpy (numerical python) предназначена для эффективной работы с линейной алгеброй.
Многозадачность встроенного типа list делает его неудобным и медленным в наукоёмких вычислениях.
Библиотека numpy предоставляет собственный тип данных, более "близкий" к стандартным массивам.
Большинство ресурсоёмких операций выполняется с помощью библиотек языков Си и Фортрана, обёрткой над которыми numpy и является.
Обычно библиотеку numpy импортируют под именем np.
Примеры работы с векторами
>>> import numpy as np
array([ 0, 1, 2, 3, -10])
>>> a = np.array([0, 1, 2, 3, -10], dtype=np.float) # dtype является необязательным параметром
>>> a
array([ 0., 1., 2., 3., -10.])
>>> b = np.array([1, 4, 5, 6, 8], dtype=np.float)
>>> a
array([ 0., 1., 2., 3., -10.])
>>> b
>>> a + b
array([ 1., 5., 7., 9., -2.])
>>> a - b
array([ -1., -3., -3., -3., -18.])
>>> a * b
array([ 0., 4., 10., 18., -80.])
>>> a / b
array([ 0. , 0.25, 0.4 , 0.5 , -1.25])
>>> a.dot(b) # скалярное произведение
-48.0
>>> np.sum(a * b)
-48.0
Некоторые часто используемые конструкторы
>>> np.linspace(0, 10, 5) # равномерная сетка
array([ 0. , 2.5, 5. , 7.5, 10. ])
>>> np.linspace(0, 10, 5, dtype=np.int)
array([ 0, 2, 5, 7, 10])
>>> np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # арифметическая прогрессия
>>> np.arange(1, 10, 3)
array([1, 4, 7])
>>> np.random.rand(10) # вектор из 10 случайных чисел
array([0.15588698, 0.01149716, 0.51116519, 0.21913986, 0.37452467,
0.76447507, 0.09531357, 0.62435988, 0.63161721, 0.32714768])
Работа с матрицами
>>> a = np.array([1, 2])
>>> A = np.array([[1, 2], [3, 4]]) # матрица 2x2
>>> A
array([[1, 2],
[3, 4]])
>>> A.dot(a) # умножение матрицы на вектор
array([ 5, 11])
>>> np.linalg.solve(A, [5, 11]) # решение системы уравнений Ax = b, где b = [5, 11]
array([1., 2.])
>>> A_inv = np.linalg.inv(A) # вычисление обратной матрицы A^-1
>>> A.dot(A_inv) # проверяем, что A A^-1 = E
array([[1.0000000e+00, 0.0000000e+00],
[8.8817842e-16, 1.0000000e+00]])
>>> np.linalg.det(A) # вычисление детерминанта матрицы A
-2.0000000000000004
Построение научной графики - модуль matplotlib
Библиотека matplotlib служит для построения высококачественной научной графики и предоставляет программисту полный контроль над содержимым: типы графиков, полотно, цвета, шрифты, подписи...
В этом разделе мы рассмотрим только базовую работу.
Для построения графиков пользуются модулем pyplot, необходимо его импортировать, обычно модулю дают синоним plt
>>> import matplotlib.pyplot as plt
>>> help(plt)
Help on module matplotlib.pyplot in matplotlib:
NAME
matplotlib.pyplot
DESCRIPTION
`matplotlib.pyplot` is a state-based interface to matplotlib. It provides
a MATLAB-like way of plotting.
Как видно из сообщения документации, pyplot является одним из интерфейсов работы. "state-based interface" означает, что в библиотеке хранится состояние всех настроек построения: цвета, размеры и т.п. Это позволяет работать с графикой "из коробки".
Чтобы добавить график, воспользуйтесь функцией plt.plot(x, y)
>>> plt.plot([0, 1, 2, 3], [0, 1, 4, 9])
[<matplotlib.lines.Line2D object at 0x10f9d5750>]
Эта функция возвращает объект двухмерного графика и если нам не нужно с ним больше работать, то можно его не сохранять в переменную.
Чтобы вывести построение на экран, необходимо вызвать функцию plt.show()
>>> plt.show()
plt.show() выводит изображение на один из терминалов, обычно это оконные интерфейсы QT5 или X11.
В них доступно сохранение изображения и навигация с масштабированием видимой области (это можно использовать, например, для графического решения системы уравнений).
Сохранить график программно можно с вызовом функции plt.savefig(fname), для которой обязательный аргумент - файл, в которой сделать запись.
С помощью дополнительных аргументов можно контролировать качество изображения.
Ниже дан пример построения двух графиков
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 4*np.pi, 200) # отрезок [0, 4π] из 200 точек
yline = 0.04 * x
ysin = np.exp(-x/(2*np.pi))*np.sin(x) # exp(-x/2π) sin(x)
# добавление графиков
plt.plot(x, ysin, label='затухающее колебание', color='red', linewidth=2)
plt.plot(x, yline, label='прямая', color='blue', linewidth=3)
# название всего графика и подписи к осям
plt.title('Пример построения двух графиков')
plt.xlabel('абсцисса')
plt.ylabel('ордината')
# ограничение видимой области графика
plt.xlim(0, 12)
plt.ylim(-1, 1)
# отметки на абсциссе, первый аргумент - положения, второй - подписи
plt.xticks(np.arange(0, 5*np.pi, np.pi), [ str(i) + 'π' for i in range(6) ])
plt.grid() # сетка по отметкам на осях
plt.legend() # подписи графиков
plt.show()
# plt.savefig('temp.png', dpi=90) # расскомментировать для сохранения картинки
Результат должен быть похож на это
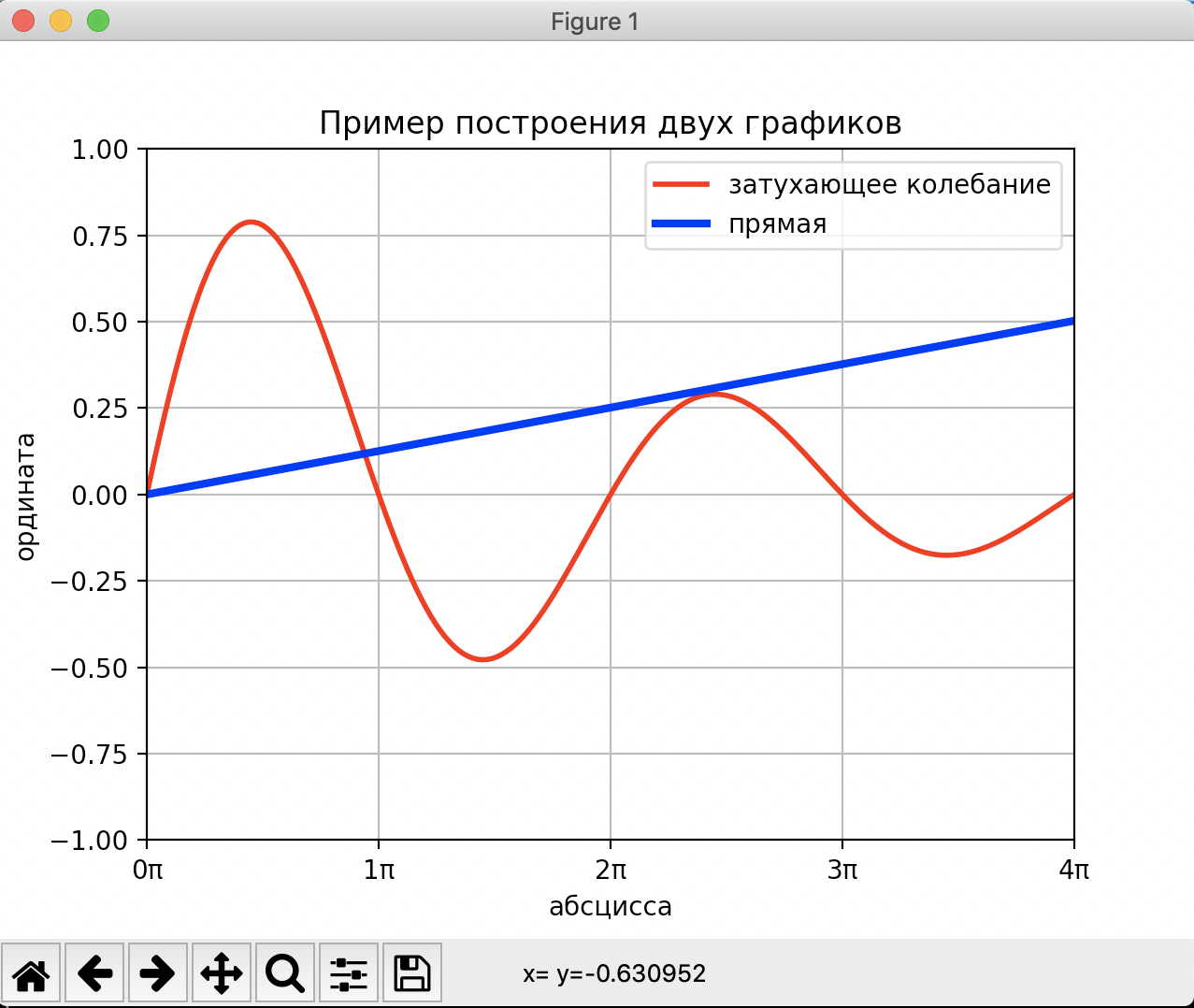
Ссылки
- Официальный сайт matplotlib https://matplotlib.org/index.html
- Вводная информация https://matplotlib.org/tutorials/introductory/usage.html, особенно ценна картинка с терминами "Parts of a Figure"
- Примеры графиков https://matplotlib.org/gallery/index.html
Упражнения
Все упражнения необходимо выполнить.
Упражнение 1 - Работа с файлами
Скачайте входной файл task1.txt.
В каждой его строчке содержится по несколько чисел через пробел.
Вам необходимо создать файл out.txt, в каждой строчке которого содержится среднее арифметическое чисел из соответствующей строчки входного файла.
Упражнение 2 - Подсчёт асимптотик
Проверьте асимптотики следующих групп алгоритмов
- алгоритмы сортировки: вставками, кучей, встроенная
list.sort() - добавление элемента в начало:
list.insert(x, 0)иdeque.appendleft(), взятие элемента из начала:deque.popleft()иlist.pop(0) - поиск элемента: операции elem in list и elem in set
Для каждой группы постройте график асимптотики - зависимости времени работы алгоритма от характерного масштаба задачи.
Задачи
Количество необходимых для решения задач уточните у своего преподавателя!
Снежинки!
Напишите две программы. Первая должна строить кривую Коха заданной глубины. Вторая - снежинку Коха (плоская фигура).
Калькулятор
Напишите калькулятор -- программу, считывающую арифметическое выражение в инфиксной записи, и вычисляющую результат выражения. Поддерживаемые операции: сложение, вычитание, деление и умножение.
Также добавьте в ваш калькулятор поддержку выражений со скобками.
Пример работы:
>>> solve('5 - 3 * (8 + 1)')
-22
Перед выполнением задачи ознакомьтесь с https://mipt-cs.github.io/python3-2017-2018/labs/lab14.html.
Дешифрация Цезаря
В файле ceasar.txt содержится зашифрованное кодом Цезаря сообщение. Расшифруйте его.
Напишите программу, которая автоматически расшифровывает подобные сообщения.
Шифр Цезаря -- сдвиговый шифр. После выбора сдвига N каждая буква сообщения заменяется на букву, стоящую на N позиций правее в алфавите (при этом алфавит закольцовывается). Например, при сдвиге 2 в русском алфавите произойдут замены А → В, Б → Г, ..., Ю → А, Я → Б и строка 'AБЮЯ' перейдёт в 'ВГАБ'.
Найди рыбу
Скачайте входной файл find_a_fish.txt. В нём находятся 4 аминокислотных последовательности белка, выполняющего одну и ту же функцию, но присутсвующие в различных организмах. Три из них получены из млекопитающих, одна из них - из рыбы. Вычислив редакционное расстояние Левенштейна, сделайте предположение, последовательность с каким номером принадлежит рыбе.
Задача трёх тел
Решите численно задачу трёх тел на плоскости. Тела считать материальными точками. Известны массы тел, начальные положения и начальные скорости. Тела взаимодействуют только гравитационно, внешние силы осутствуют. Для численного решения динамических уравнений можете воспользоваться схемой Эйлера, либо схемой более высокого порядка точности.
Столкновение тел можно не рассматривать.
Рекомендуется создать две программы
- первая -- ресурсоёмкая, производит вычисления положений тел на промежутке времени от 0 до T и записывает эти положения в выходной файл
- вторая анимацинно строит полёт тел по файлу данных первой программы (для построения анимации посмотрите примеры использования matplotlib.animation.FuncAnimation)
