Машинное обучение (Machine Learning)

Общая постановка задачи обучения по прецедентам

Дано конечное множество прецедентов (объектов, ситуаций), по каждому из которых собраны (измерены) некоторые данные. Данные о прецеденте называют также его описанием. Совокупность всех имеющихся описаний прецедентов называется обучающей выборкой. Требуется по этим частным данным выявить общие зависимости, закономерности, взаимосвязи, присущие не только этой конкретной выборке, но вообще всем прецедентам, в том числе тем, которые ещё не наблюдались. Говорят также о восстановлении зависимостей по эмпирическим данным — этот термин был введён в работах Вапника и Червоненкиса.

Наиболее распространённым способом описания прецедентов является признаковое описание. Фиксируется совокупность n показателей, измеряемых у всех прецедентов. Если все n показателей числовые, то признаковые описания представляют собой числовые векторы размерности n. Возможны и более сложные случаи, когда прецеденты описываются временными рядами или сигналами, изображениями, видеорядами, текстами, попарными отношениями сходства или интенсивности взаимодействия, и т. д.

Для решения задачи обучения по прецедентам в первую очередь фиксируется модель восстанавливаемой зависимости. Затем вводится функционал качества, значение которого показывает, насколько хорошо модель описывает наблюдаемые данные. Алгоритм обучения (learning algorithm) ищет такой набор параметров модели, при котором функционал качества на заданной обучающей выборке принимает оптимальное значение. Процесс настройки (fitting) модели по выборке данных в большинстве случаев сводится к применению численных методов оптимизации.

Основные типы задач

1. Обучение с учителем (Supervised Machine Learning): наиболее распространённый случай. Каждый прецедент представляет собой пару «объект, ответ». Требуется найти функциональную зависимость ответов от описаний объектов и построить алгоритм, принимающий на входе описание объекта и выдающий на выходе ответ. Функционал качества обычно определяется как средняя ошибка ответов, выданных алгоритмом, по всем объектам выборки. Задачи обучения с учителем делятся на следующие типы :

   • Классификация: отличается тем, что множество допустимых ответов конечно. Их называют метками классов (class label). Класс — это множество всех объектов с данным значением метки. Пример - задача о возврате кредита клиентом банка.

     

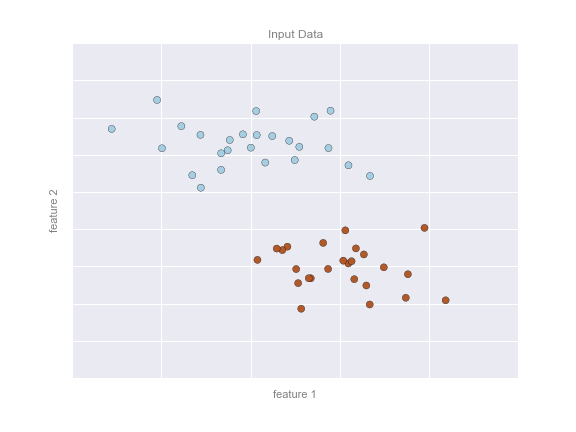
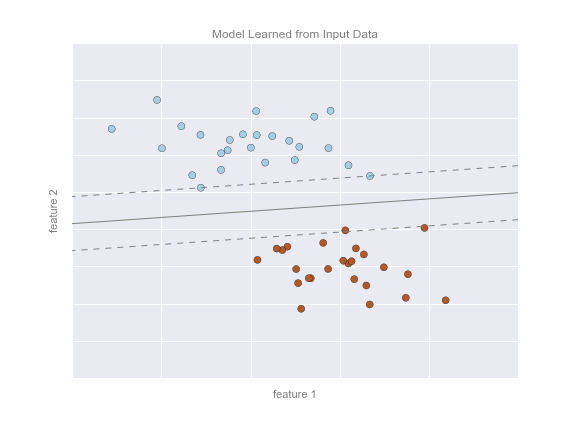
   • Регресиия: отличается тем, что допустимым ответом является действительное число или числовой вектор. Пример - максимальный размер кредита для клиента.

     

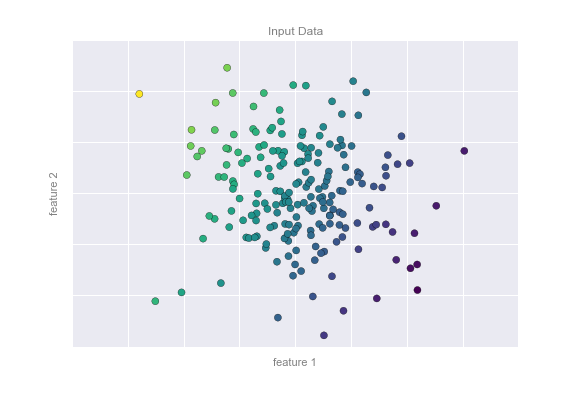
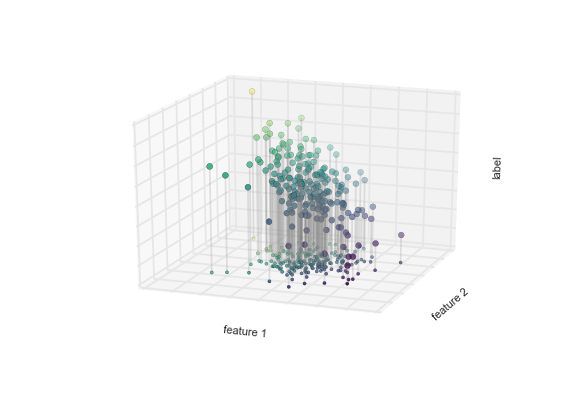
Ранжирование (ranking) и прогнозирование (forecasting) - другие примеры задач , сводящихся к классификации и регрессии.

• Ранжирование отличается тем, что ответы надо получить сразу на множестве объектов, после чего отсортировать их по значениям ответов.
• Прогнозирование отличается тем, что объектами являются отрезки временных рядов, обрывающиеся в тот момент, когда требуется сделать прогноз на будущее.

2. Обучение без учителя (Unsupervised Machine Learning): В этом случае ответы не задаются, и требуется искать зависимости между объектами. Пример: банк хочет разделить клиентов на группы собразно их поведению.

   • кластеризация (clustering) заключается в том, чтобы сгруппировать объекты в кластеры, используя данные о попарном сходстве объектов. Функционалы качества могут определяться по-разному, например, как отношение средних межкластерных и внутрикластерных расстояний.

     

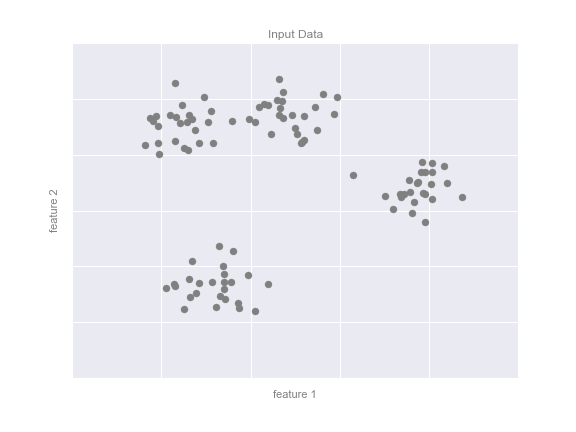
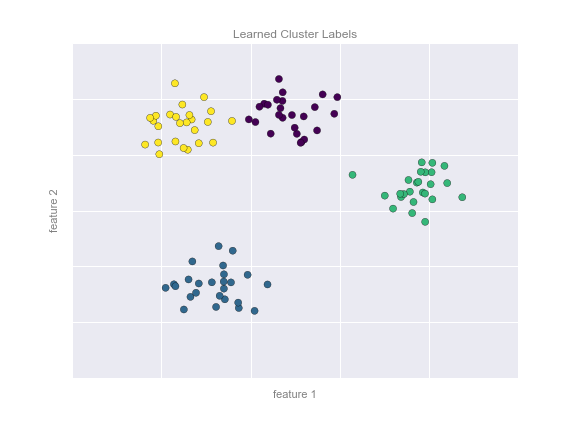
   • поиск ассоциативных правил (association rules learning). Исходные данные представляются в виде признаковых описаний. Требуется найти такие наборы признаков, и такие значения этих признаков, которые особенно часто (неслучайно часто) встречаются в признаковых описаниях объектов.

   • снижение размерности (dimensionality reduction) заключается в том, чтобы по исходным признакам с помощью некоторых функций преобразования перейти к наименьшему числу новых признаков, не потеряв при этом никакой существенной информации об объектах выборки. В классе линейных преобразований наиболее известным примером является метод главных компонент .

     

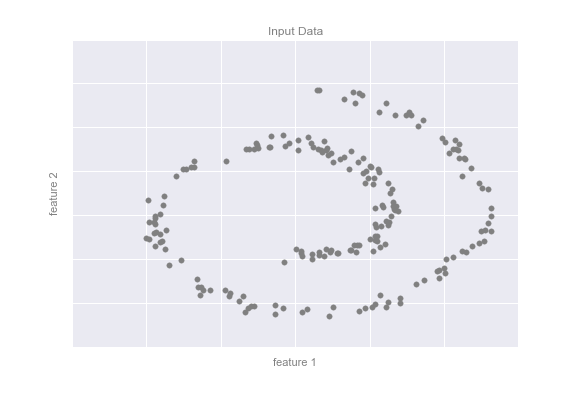
3. Обучение с подкреплением (Reinforcement Learning): считается основной надеждой "истинного" искусственного интеллекта. Считается, что потенциал этого подхода огромен. Хотя это на данный момент самая сложная часть теории анализа данных. Роль объектов играют пары «ситуация, принятое решение», ответами являются значения функционала качества, характеризующего правильность принятых решений (реакцию среды). Как и в задачах прогнозирования, здесь существенную роль играет фактор времени. Примеры прикладных задач: формирование инвестиционных стратегий, автоматическое управление технологическими процессами, самообучение роботов.

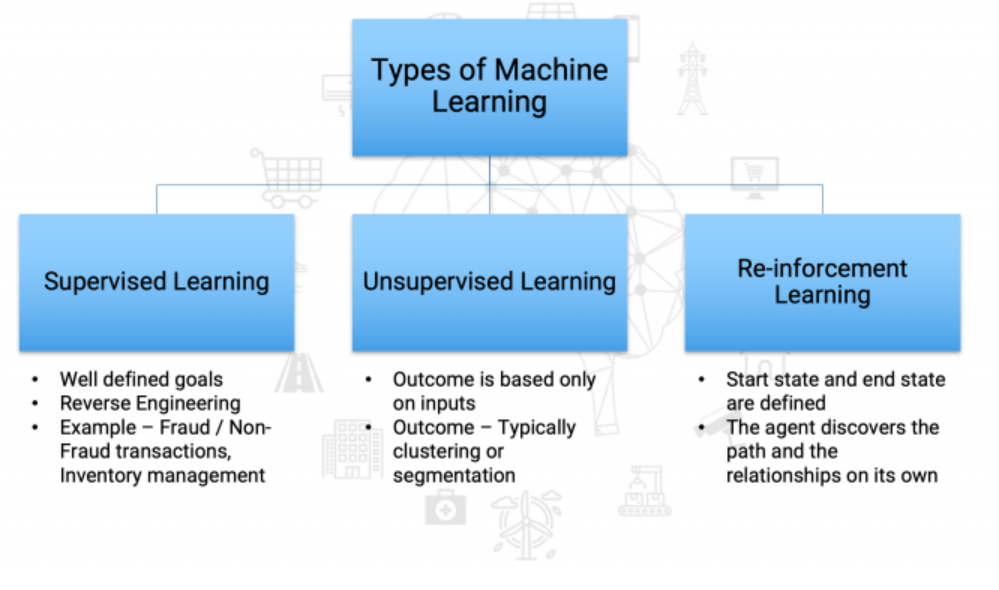
• Картинка с сайта https://courses.analyticsvidhya.com/courses/Machine-Learning-Certification-Course-for-Beginners?utm_source=blog_navbar&utm_medium=start_here_button

В эту красивую схему укладываются все или почти все задачи машинного обучения. Другие типы представляют собой комбинации и модификации перечисленных. Примеры:

• Частичное обучение (semi-supervised learning) занимает промежуточное положение между обучением с учителем и без учителя. Каждый прецедент представляет собой пару «объект, ответ», но ответы известны только на части прецедентов. Пример прикладной задачи — автоматическая рубрикация большого количества текстов при условии, что некоторые из них уже отнесены к каким-то рубрикам. К частичному обучению сводится также трансдуктивное обучение (transductive learning) - когда дана конечная обучающая выборка прецедентов и требуется по этим частным данным сделать предсказания отностительно других частных данных.
• Метаобучение (meta-learning или learning-to-learn) - когда прецедентами являются ранее решённые задачи обучения. Требуется определить, какие из используемых в них эвристик работают более эффективно. Конечная цель — обеспечить постоянное автоматическое совершенствование алгоритма обучения с течением времени.

Обучение с учителем и без учителя

В зависимости от данных алгоритмы машинного обучения могут быть поделены на те, что обучаются с учителем и без учителя (supervised & unsupervised learning). В задачах обучения без учителя имеется выборка, состоящая из объектов, описываемых набором признаков. В задачах обучения с учителем вдобавок к этому для каждого объекта некоторой выборки, называемой обучающей, известен целевой признак – по сути это то, что хотелось бы прогнозировать для прочих объектов, не из обучающей выборки. Т.е в задачах МО с учителем на обучающей выборке у нас есть “правильные” ответы, а когда задача без учителя - то нет

Метрики качества

Наконец, третья абстракция в машинном обучении – это метрика оценки производительности алгоритмов. Такие метрики различаются для разных задач и алгоритмов. Пока скажем, что самая простая метрика качества алгоритма, решающего задачу классификации – это доля правильных ответов (accuracy, не называйте ее точностью, этот перевод зарезервирован под другую метрику, precision) – то есть попросту доля верных прогнозов алгоритма на тестовой выборке.

Основные подходы

Простейший линейный случай

Пожалуй, лучшее философское введение в машинное обучение дано в книге Домингоса Верховный алгоритм

Там выделены 5 основных идеологий поиска идеального , "верховного " алгоритма обучения.

1. Индукционный
2. Сетевой
3. Эволюционный (генетические алгоритмы)
4. Байесов (вероятностный) - восстановление вероятностных распределений и сети доверия
5. Метрический

Пример задачи Классификации

Начнем с задач Классификации, хотя зачастую эти задачи можно свести к задаче регрессии

Знакомство с данными

Хранятся как стандартный набор внутри библиотеки Scikit-learn

from sklearn.datasets import load_iris
iris_dataset = load_iris()

print("Keys of iris_dataset:\n", iris_dataset.keys())

Keys of iris_dataset:
 dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])

print(iris_dataset['DESCR'][:193] + "\n...")

Набор данных про ирисы (dataset)

Характеристики набора данных:

Всего прецедентов:
	150 (по 50 в каждом из 3 классов)
всего признаков:
	4 числовых

Названия классов

print("Target names:", iris_dataset['target_names'])

Target names: ['setosa' 'versicolor' 'virginica']

Названия признаков

print("Feature names:\n", iris_dataset['feature_names'])

Feature names:
 ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

print("Type of data:", type(iris_dataset['data']))

Type of data: <class 'numpy.ndarray'>

print("Shape of data:", iris_dataset['data'].shape)

Shape of data: (150, 4)

Пример из набора данных

print("First five rows of data:\n", iris_dataset['data'][:5])

First five rows of data:
 [[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]]

print("Type of target:", type(iris_dataset['target']))

Type of target: <class 'numpy.ndarray'>

print("Shape of target:", iris_dataset['target'].shape)

Shape of target: (150,)

Известные ответы для прецедентов (классы, к которым они принадлежат).

print("Target:\n", iris_dataset['target'])

Target:
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

Измерение качества: обучающая и контрольная выборки

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
     iris_dataset['data'], iris_dataset['target'], random_state=0)

print("X_train shape:", X_train.shape)
print("y_train shape:", y_train.shape)

X_train shape: (112, 4)
y_train shape: (112,)

print("X_test shape:", X_test.shape)
print("y_test shape:", y_test.shape)

X_test shape: (38, 4)
y_test shape: (38,)

Предобработка данных (preconditioning)

# create dataframe from data in X_train
# label the columns using the strings in iris_dataset.feature_names
iris_dataframe = pd.DataFrame(X_train, columns=iris_dataset.feature_names)
# create a scatter matrix from the dataframe, color by y_train
pd.plotting.scatter_matrix(iris_dataframe, c=y_train, figsize=(15, 15),
                                    marker='o', hist_kwds={'bins': 20}, s=60,
                                    alpha=.8, cmap=mglearn.cm3)

array([[<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE868F9C88>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE869714C8>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE869A5D48>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE869DFE08>],
         [<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86A18E48>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86A4FEC8>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86A88F88>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86AC8088>],
         [<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86ACEC48>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86B06D88>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86B71188>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86BAA208>],
         [<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86BE22C8>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86C1A388>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86C54408>,
           <matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86C8C3C8>]],
        dtype=object)

Мой первый классификатор: k-Nearest Neighbors

Создаём классификатор по 1 ближайшему соседу

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)

Обучаем его, вызывая функцию fit

knn.fit(X_train, y_train)

Предсказание

Создаём искусственный прецедент для классификации

X_new = np.array([[5, 2.9, 1, 0.2]])
print("X_new.shape:", X_new.shape)

X_new.shape: (1, 4)

Узнаём прежссказанное значение для него. которое даёт наш обученный классификатор

prediction = knn.predict(X_new)
print("Prediction:", prediction)
print("Predicted target name:",
         iris_dataset['target_names'][prediction])

Prediction: [0]
Predicted target name: ['setosa']

Оценка качества модели

Узнаем ответ обученного классификатора на контрольной выборке

y_pred = knn.predict(X_test)
print("Test set predictions:\n", y_pred)

Test set predictions:
 [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
 2]

print("Test set score: {:.2f}".format(np.mean(y_pred == y_test)))

Test set score: 0.97

print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))

Test set score: 0.97

X_train, X_test, y_train, y_test = train_test_split(
     iris_dataset['data'], iris_dataset['target'], random_state=0)

knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)

print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))

Test set score: 0.97

Выбор параметров модели и кросс-валидация

Главная задача обучаемых алгоритмов – их способность обобщаться, то есть хорошо работать на новых данных. Поскольку на новых данных мы сразу не можем проверить качество построенной модели (нам ведь надо для них сделать прогноз, то есть истинных значений целевого признака мы для них не знаем), то надо пожертвовать небольшой порцией данных, чтоб на ней проверить качество модели.

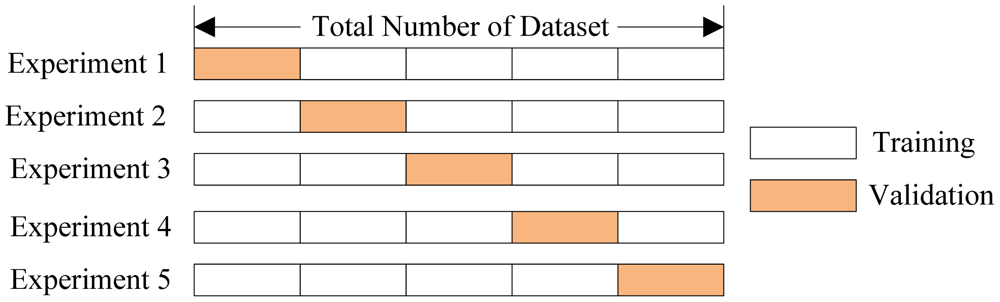
Чаще всего это делается одним из 2 способов: * отложенная выборка (held-out/hold-out set). При таком подходе мы оставляем какую-то долю обучающей выборки (как правило от 20% до 40%), обучаем модель на остальных данных (60-80% исходной выборки) и считаем некоторую метрику качества модели (например, самое простое – долю правильных ответов в задаче классификации) на отложенной выборке. * кросс-валидация (cross-validation, на русский еще переводят как скользящий или перекрестный контроль). Тут самый частый случай – K-fold кросс-валидация.

Тут модель обучается K раз на разных (K-1) подвыборках исходной выборки (белый цвет), а проверяется на одной подвыборке (каждый раз на разной, оранжевый цвет). Получаются K оценок качества модели, которые обычно усредняются, выдавая среднюю оценку качества классификации/регрессии на кросс-валидации.

Кросс-валидация дает лучшую по сравнению с отложенной выборкой оценку качества модели на новых данных. Но кросс-валидация вычислительно дорогостоящая, если данных много.

Кросс-валидация – очень важная техника в машинном обучении (применяемая также в статистике и эконометрике), с ее помощью выбираются гиперпараметры моделей, сравниваются модели между собой, оценивается полезность новых признаков в задаче и т.д.

Задание:

Оценить работу kNN классификатора для Ирисов (или любого другого набора данных) с помощью Перекрестного контроля с разными параметрами разбиения выборки на обучающую и контрольную.