Пострение графиков

Запись алгебраических выражений

Фундаментальная задача программирования — вычисление математических и, в частности, алгебраических функций. Казалось бы, что проще? Однако, запись выражения на языке математики не принимается напрямую языком программирования. Выражение нужно написать в виде, который будет понятен тому или иному языку программирования.

Например, y = x², должно быть записано как y = x*x или y = x**2.

Упражнение №1

Запишите выражение, заданное формулой, в виде, подходящем для языка Python.

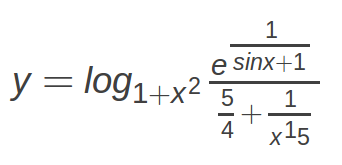
и найдите его значения в точках 1, 10, 1000.

Для вычисления математических функций мы не будем использовать стандартную библиотеку math. Т.к. она не работает с векторами. В нашем случае разумней обратить внимание на библиотеку numpy. Данная библиотека обеспечивает удобную работу с векторам.

Т.е., если у нас есть вектор x=[1, 2, 3, 4] и мы вызовим numpy.log(x), то логарифм будет взят от каждого элемента списка и возвращен будет список значений.

Аналогичная функция в модуля math ожидает число, т.е. нельзя сделать math.log(x), нужно делать math.log(x[0]) и т.д.

Традиционно библиотека numpy подключается командой:

import numpy as np

Данный вызов сообщает, что подключить numpy под псевдонимом np. Это делается, чтобы не писать каждый раз:

numpy.cos(x)

А писать:

np.cos(x)

Такой код, с более коротким именем библиотеки, элементарно, проще читать.

Основные математические функции и константы функии, которые нам понадобятся из numpy:

Функция библиотеки math	Математическая функция
np.pi	Число pi
np.e	Число e
np.cos	Косинус
np.sin	Синус
np.tan	Тангенс
np.acos	Арккосинус
np.asin	Арксинус
np.atan	Арктангенс
np.exp	Экспонента
np.log	Логарифм

Функция log вычисляет натуральный логарифм. Чтобы вычислить логарифм по другому основанию, нужно воспользоваться формулой перехода. Например, если мы хотим получить логарифм x по основанию 2, нужно написать:

np.log(x) / np.log(2)

Построение графиков

matplotlib - набор дополнительных модулей (библиотек) языка Python. Предоставляет средства для построения самых разнообразных 2D графиков и диаграмм данных. Отличается простотой использования — для построения весьма сложных и красочно оформленных диаграмм достаточно нескольких строк кода. При этом качество получаемых изображений более чем достаточно для их публикования. Также позволяет сохранять результаты в различных форматах, например Postscript, и, соответственно, вставлять изображения в документы TeX. Предоставляет API для встраивания своих графических объектов в приложения пользователя.

Пример построения графика функции:

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10.01, 0.01)
plt.plot(x, x**2)
plt.show()

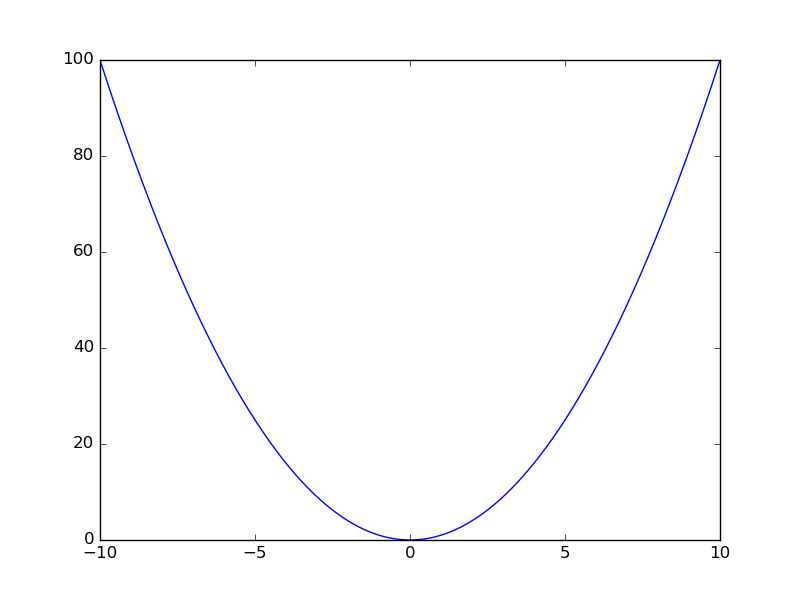
На одном рисунке можно построить несколько графиков функций:

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10.01, 0.01)
plt.plot(x, np.sin(x), x, np.cos(x), x, -x)
plt.show()

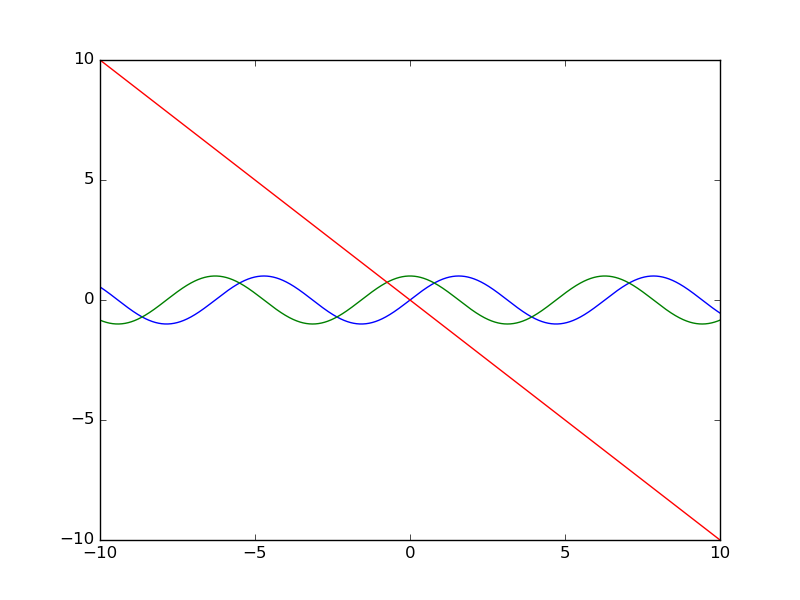
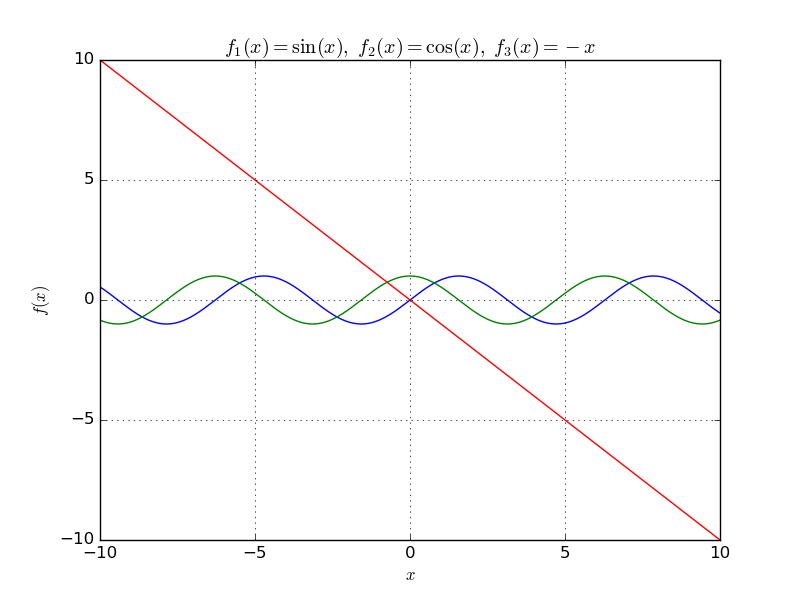
Также довольно просто на график добавить служебную информацию и отобразить сетку:

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10.01, 0.01)
plt.plot(x, np.sin(x), x, np.cos(x), x, -x)
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.title(r'$f_1(x)=\sin(x),\ f_2(x)=\cos(x),\ f_3(x)=-x$')
plt.grid(True)
plt.show()

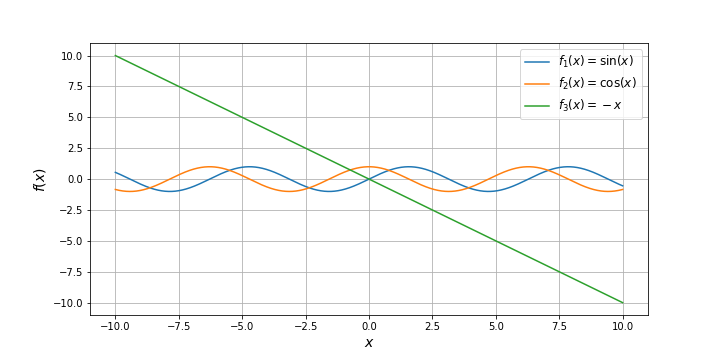
Или используя legend(), где можно указать место расположения подписей к кривым на графике в параметре loc. Подписи могут быть явно переданы legend((line1, line2, line3), ('label1', 'label2', 'label3')) или могут быть переданы в аргумет label, как в примере ниже. Чтобы сохранить график нужно воспользоваться savefig(figure_name), где figure_name явлется строкой назания файла с указанием расширения. Для текстовых полей можно изменять шрифт (fontsize), для большей читаемости графика, а его размер указывается с помощью figure(figsize=(10, 5)).

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10.01, 0.01)
plt.figure(figsize=(10, 5))
plt.plot(x, np.sin(x), label=r'$f_1(x)=\sin(x)$')
plt.plot(x, np.cos(x), label=r'$f_2(x)=\cos(x)$')
plt.plot(x, -x, label=r'$f_3(x)=-x$')
plt.xlabel(r'$x$', fontsize=14)
plt.ylabel(r'$f(x)$', fontsize=14)
plt.grid(True)
plt.legend(loc='best', fontsize=12)
plt.savefig('figure_with_legend.png')
plt.show()

Текстовые поля в matplotlib могут содержать разметку LaTeX, заключенную в знаки $. Буква r перед кавычками говорит python, что символ "\" следует оставить как есть и не интерпретировать как начало спецсимвола (например, перевода строки - "\n").

Работа с matplotlib основана на использовании графических окон и осей (оси позволяют задать некоторую графическую область). Все построения применяются к текущим осям. Это позволяет изображать несколько графиков в одном графическом окне. По умолчанию создаётся одно графическое окно figure(1) и одна графическая область subplot(111) в этом окне. Команда subplot позволяет разбить графическое окно на несколько областей. Она имеет три параметра: nr, nc, np. Параметры nr и nc определяют количество строк и столбцов на которые разбивается графическая область, параметр np определяет номер текущей области (np принимает значения от 1 до nr*nc). Если nr*nc<10, то передавать параметры nr, nc, np можно без использования запятой. Например, допустимы формы subplot(2,2,1) и subplot(221).

     import numpy as np
     import matplotlib.pyplot as plt
     x = np.arange(-10, 10.01, 0.01)
t = np.arange(-10, 11, 1)

     #subplot 1
     sp = plt.subplot(221)
     plt.plot(x, np.sin(x))
     plt.title(r'$\sin(x)$')
     plt.grid(True)

     #subplot 2
     sp = plt.subplot(222)
     plt.plot(x, np.cos(x), 'g')
     plt.axis('equal')
     plt.grid(True)
     plt.title(r'$\cos(x)$')

     #subplot 3
     sp = plt.subplot(223)
     plt.plot(x, x**2, t, t**2, 'ro')
     plt.title(r'$x^2$')

     #subplot 4
     sp = plt.subplot(224)
     plt.plot(x, x)
     sp.spines['left'].set_position('center')
     sp.spines['bottom'].set_position('center')
     plt.title(r'$x$')

     plt.show()

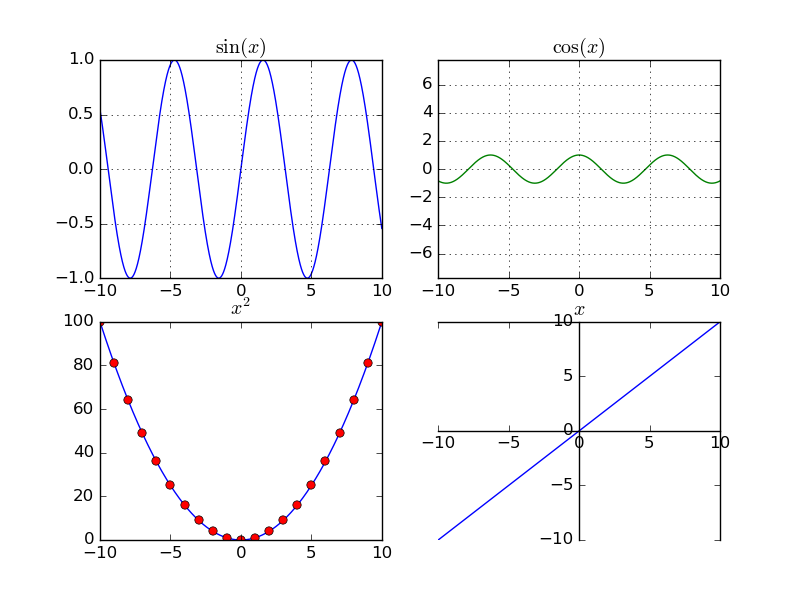
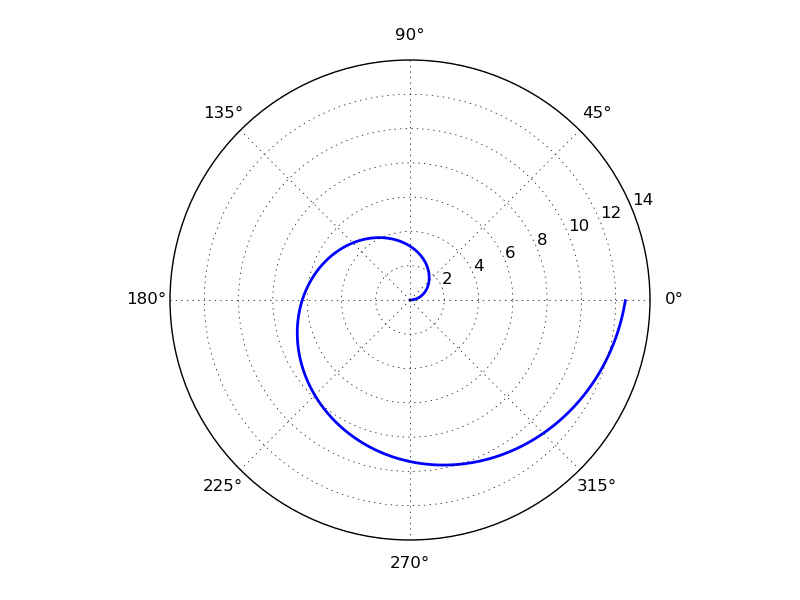
График может быть построен в полярной системе координат, для этого при создании subplot необходимо указать параметр polar=True:

import numpy as np
import matplotlib.pyplot as plt
plt.subplot(111, polar=True)
phi = np.arange(0, 2*np.pi, 0.01)
rho = 2*phi
plt.plot(phi, rho, lw=2)
plt.show()

Или может быть задан в параметрической форме (для этого не требуется никаких дополнительных действий, поскольку два массива, которые передаются в функцию plot воспринимаются просто как списки координат точек, из которых состоит график):

import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0, 2*np.pi, 0.01)
r = 4
plt.plot(r*np.sin(t), r*np.cos(t), lw=3)
plt.axis('equal')
plt.show()

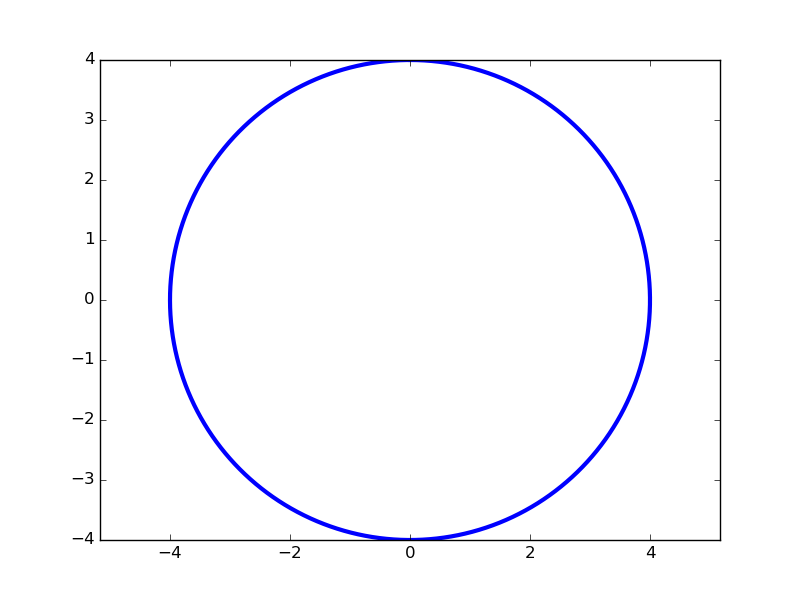
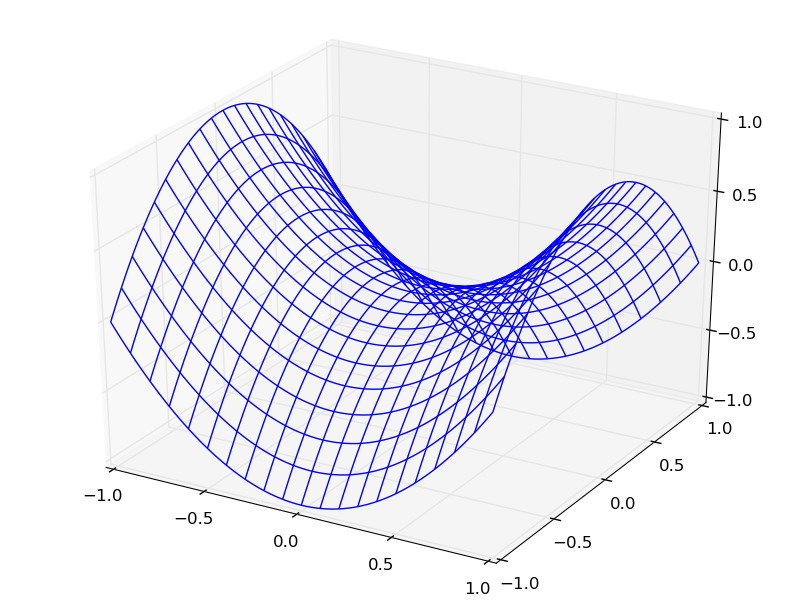
График функции двух переменных может быть построен, например, так:

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
ax = axes3d.Axes3D(plt.figure())
i = np.arange(-1, 1, 0.01)
X, Y = np.meshgrid(i, i)
Z = X**2 - Y**2
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
plt.show()

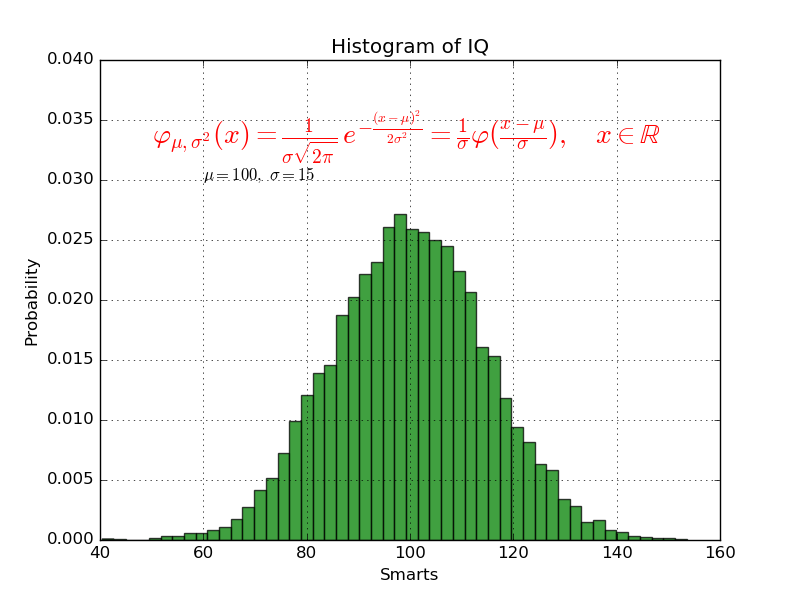
Добавление текста на график: Команду text() можно использовать для добавления текста в произвольном месте (по умолчанию координаты задаются в координатах активных осей), а команды xlabel(), ylabel() и title() служат соответственно для подписи оси абсцисс, оси ординат и всего графика. Для более полной информации смотрите «Text introduction» раздел на оф. сайте.

import numpy as np
import matplotlib.pyplot as plt
mu, sigma = 100, 15
x = mu + sigma * np.random.randn(10000)
# the histogram of the data
n, bins, patches = plt.hist(x, 50, density=True, facecolor='g', alpha=0.75)

plt.xlabel('Smarts')
plt.ylabel('Probability')
plt.title('Histogram of IQ')
plt.text(60, .030, r'$\mu=100,\ \sigma=15$')
plt.text(50, .033, r'$\varphi_{\mu,\sigma^2}(x) = \frac{1}{\sigma\sqrt{2\pi}} \,e^{ -\frac{(x- \mu)^2}{2\sigma^2}} = \frac{1}{\sigma} \varphi\left(\frac{x - \mu}{\sigma}\right),\quad x\in\mathbb{R}$', fontsize=20, color='red')
plt.axis([40, 160, 0, 0.04])
plt.grid(True)
plt.show()

plot() — универсальная команда и в неё можно передавать произвольное количество аргументов. Например, для того, чтобы отобразить y в зависимости от x, можно выполнить команду:

import matplotlib.pyplot as plt
plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.show()

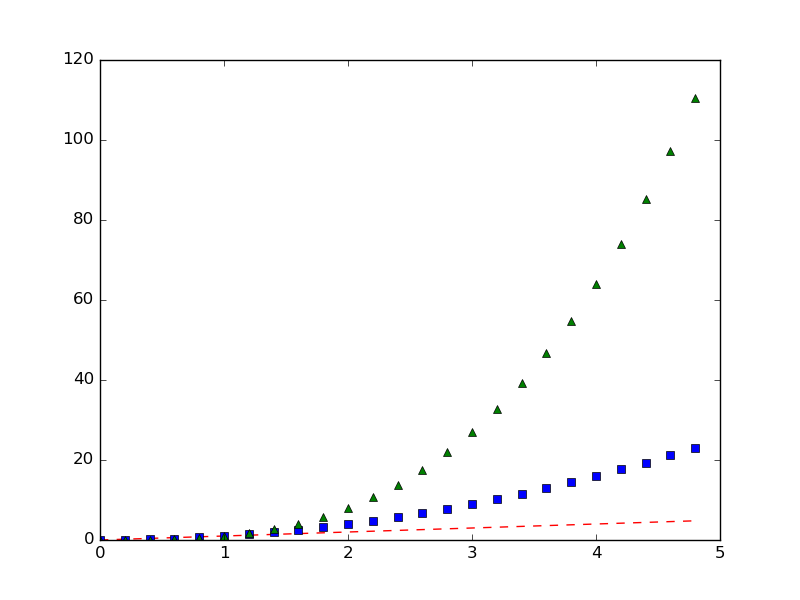
Каждую последовательность можно отобразить своим типом точек:

import numpy as np
import matplotlib.pyplot as plt

# равномерно распределённые значения от 0 до 5, с шагом 0.2
t = np.arange(0., 5., 0.2)

# красные чёрточки, синие квадраты и зелёные треугольники
plt.plot(t, t, 'r--', t, t**2, 'bs', t, t**3, 'g^')
plt.show()

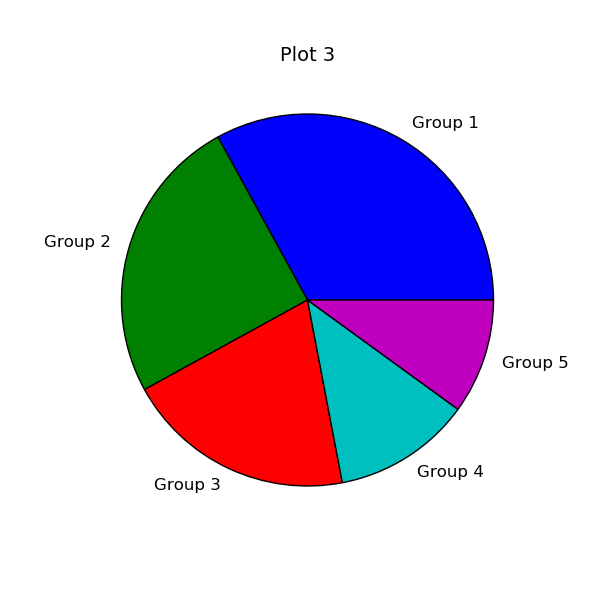
Также в matplotlib существует возможность строить круговые диаграммы:

import numpy as np
import matplotlib.pyplot as plt

data = [33, 25, 20, 12, 10]
plt.figure(num=1, figsize=(6, 6))
plt.axes(aspect=1)
plt.title('Plot 3', size=14)
plt.pie(data, labels=('Group 1', 'Group 2', 'Group 3', 'Group 4', 'Group 5'))
plt.show()

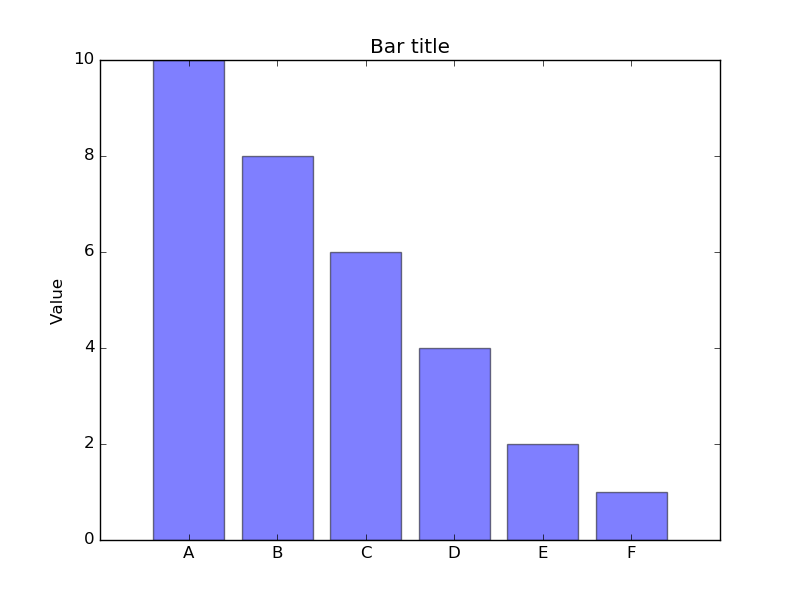
И аналогичным образом столбчатые диаграммы:

import numpy as np
import matplotlib.pyplot as plt

objects = ('A', 'B', 'C', 'D', 'E', 'F')
y_pos = np.arange(len(objects))
performance = [10,8,6,4,2,1]

plt.bar(y_pos, performance, align='center', alpha=0.5)
plt.xticks(y_pos, objects)
plt.ylabel('Value')
plt.title('Bar title')

plt.show()

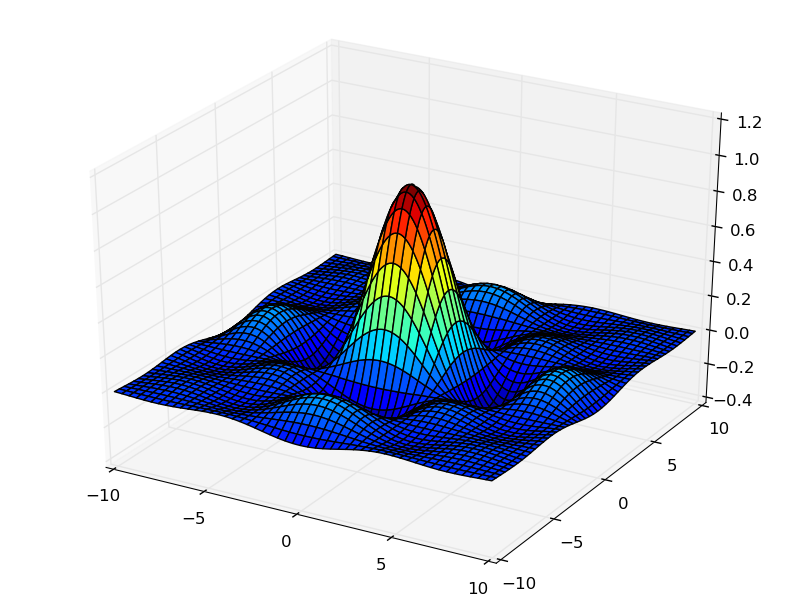
Цветовые карты используются, если нужно указать в какие цвета должны окрашиваться участки трёхмерной поверхности в зависимости от значения Z в этой области. Цветовую карту можно задать самому, а можно воспользоваться готовой. Рассмотрим использование цветовой карты на примере графика функции z(x,y)=sin(x)*sin(y)/(x*y).

import pylab
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import numpy

def makeData():
        x = numpy.arange(-10, 10, 0.1)
        y = numpy.arange(-10, 10, 0.1)
        xgrid, ygrid = numpy.meshgrid(x, y)
        zgrid = numpy.sin(xgrid)*numpy.sin(ygrid)/(xgrid*ygrid)
        return xgrid, ygrid, zgrid

x, y, z = makeData()

fig = pylab.figure()
axes = Axes3D(fig)
axes.plot_surface(x, y, z, rstride=4, cstride=4, cmap=cm.jet)
pylab.show()

Альтернативой к использованию mpl_toolkits.mplot3d является библиотека plotly, которая позволяет интерактивно взаимодействовать с графиком, поворачивая его или увеличивая некоторую область в пространсте.

Функция eval()

В Python есть встроенная функция eval(), которая выполняет строку с кодом и возвращает результат выполнения:

>>> eval("2 + 3*len('hello')")
17
>>>

Это очень мощная, но и очень опасная инструкция, особенно если строки, которые вы передаёте в eval, получены не из доверенного источника. Если строкой, которую мы решим скормить eval(), окажется "os.system('rm -rf /')", то интерпретатор честно запустит процесс удаления всех данных с компьютера.

Упражнение №3

Постройте график функции

Упражнение №4

Используя функцию eval() постройте график функции, введённой с клавиатуры. Чтобы считать данные с клавиатуры, используйте функцию input(). Попробуйте включить эффект «рисование от руки» посредством вызова plt.xkcd(). Посольку эта функция применяет некоторый набор настроек, избавиться от которых впоследствие не так просто, удобнее использовать ее как "контекстный менеджер" - это позволяет применить настройки временно, только к определенному блоку кода. Для этого используется ключевое слово with:

with plt.xkcd():
    plt.pie([70, 10, 10, 10], labels=('В комментариях', 'В Ираке', 'В Сирии', 'В Афганистане'))
    plt.title('Где ведутся самые ожесточенные бои')

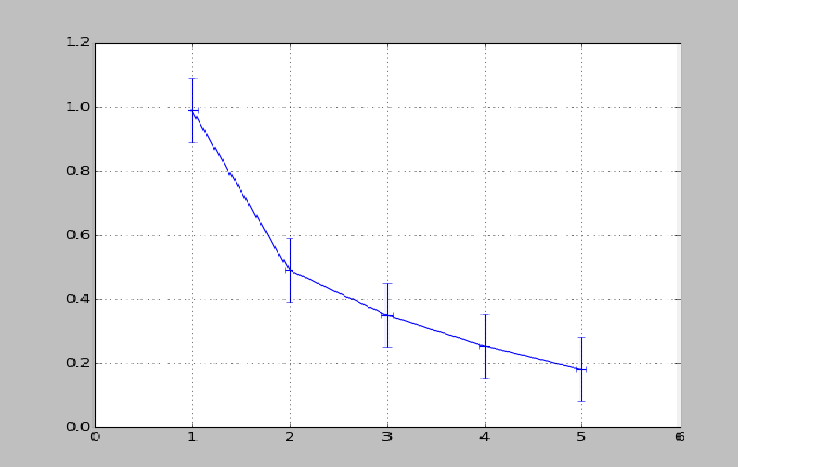
Отображение погрешностей

С помощью метода plt.errorbar можно рисовать точки с погрешностями измерений, как для лабораторных работ. Погрешности по осям абсцисс и ординат задаются в параметрах (соответственно) xerr и yerr.

import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5]
y = [0.99, 0.49, 0.35, 0.253, 0.18]
plt.errorbar(x, y, xerr=0.05, yerr=0.1)
plt.grid()
plt.show()

Альтернативой для plt.errorbar может слудить plt.fill_between, который заполняет область графика между кривыми, чтобы регулировать прозрачность используется аргумент alpha. Это число из отрезка [0, 1], на которое домножоается интенсивность цвета заполнения между кривыми.

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0, 10, 0.01)
plt.plot(x, x**2, label=r'$f = x^2$')
plt.scatter(x, x**2 + np.random.randn(len(x))*x, s=0.3)
plt.fill_between(x, 1.3*x**2, 0.7*x**2, alpha=0.3)
plt.legend(loc='best')
plt.savefig('figure_fill_between.png')
plt.show()

В уже использованном модуле numpy есть метод polyfit, позволяющий приближать данные методом наименьших квадратов. Он возвращает погрешности и коэффициенты полученного многочлена.

 x = [1, 2, 3, 4, 5, 6]
 y = [1, 1.42, 1.76, 2, 2.24, 2.5]
 p, v = np.polyfit(x, y, deg=1, cov=True)

 >>> p
 array([0.28517032, 0.80720757])
 >>> v
 array([[0.00063242, -0.00221348],
[-0.00221348, 0.00959173]])

Многочлен задается формулой p(x) = p[0] * x**deg + ... + p[deg]

Для того, чтобы не выписывать каждый раз руками эту формулу для разных степеней, есть функция poly1d, которая возвращает функцию полинома, описанного точками p. Возвращенная функция может принимать на вход не только число, но и список значений, в таком случае, будет вычислено значение функции в каждой точке списка и возвращен список результатов.

p_f = np.poly1d(p)
p_f(0.5)
p_f([1, 2, 3])