Постобработка. Выбор модели (Model Evaluation)
Содержание
- Использован материал из https://github.com/amueller/introduction_to_ml_with_python и сайта machinelearning.ru
Код к занятию notebook
полезные слайды
Перекрёстнный контроль (cross-validation)
Перекрестная проверка представляет собой статистический метод оценки обобщающей способности, который является более устойчивым и основательным, чем разбиение данных на обучающий и тестовый наборы. В перекрестной проверке данные разбиваются несколько раз и строится несколько моделей. Наиболее часто используемый вариант перекрестной проверки – k-блочная кросс-проверка (k-fold cross-validation), в которой k – это задаваемое пользователем число, как правило, 5 или 10. При выполнении пятиблочной перекрестной проверки данные сначала разбиваются на пять частей (примерно) одинакового размера, называемых блоками (folds) складками. Затем строится последовательность моделей. Первая модель обучается, используя блок 1 в качестве тестового набора, а остальные блоки (2-5) выполняют роль обучающего набора. Модель строится на основе данных, расположенных в блоках 2-5, а затем на данных блока 1 оценивается ее правильность. Затем происходит обучение второй модели, на этот раз в качестве тестового набора используется блок 2, а данные в блоках 1, 3, 4, и 5 служат обучающим набором. Этот процесс повторяется для блоков 3, 4 и 5, выполняющих роль тестовых наборов. Для каждого из этих пяти разбиений (splits) данных на обучающий и тестовый наборы мы вычисляем выбранный функционал качества.

В scikit-learn перекрестная проверка реализована с помощью функции cross_val_score модуля model_selection. Аргументами функции cross_val_score являются оцениваемая модель, обучающие данные и фактические метки. Давайте оценим качество модели LogisticRegression на наборе данных iris
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
iris = load_iris()
logreg = LogisticRegression(max_iter=1000)
scores = cross_val_score(logreg, iris.data, iris.target)
print("Cross-validation scores: {}".format(scores))
Cross-validation scores: [0.96666667 1. 0.93333333 0.96666667 1. ]
scores = cross_val_score(logreg, iris.data, iris.target, cv=5)
print("Cross-validation scores: {}".format(scores))
Cross-validation scores: [0.96666667 1. 0.93333333 0.96666667 1. ]
print("Average cross-validation score: {:.2f}".format(scores.mean()))
Average cross-validation score: 0.97
По умолчанию cross_val_score выполняет трехблочную перекрестную проверку, возвращая три значения качества. Мы можем изменить количество блоков, задав другое значение параметра cv
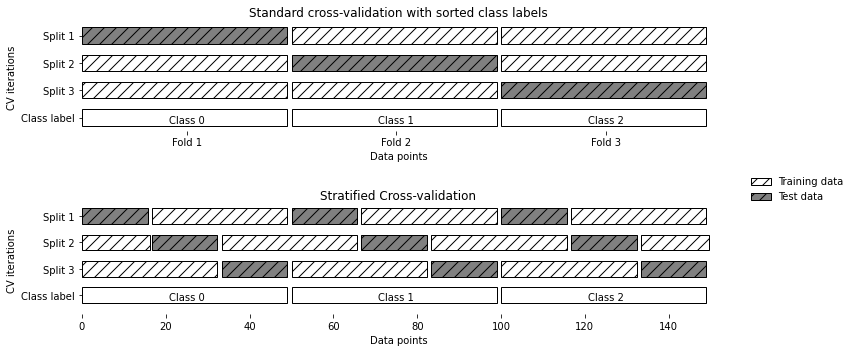
Стратифицированный перекрёстный контроль
Описанное в предыдущем разделе разбиение данных на k блоков, начиная с первого k-го блока, не всегда является хорошей идеей. Для примера давайте посмотрим на набор данных iris
from sklearn.datasets import load_iris
iris = load_iris()
print("Iris labels:\n{}".format(iris.target))
Iris labels: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
Как видно, первая треть данных – это класс 0, вторая треть – класс 1, а последняя треть – класс 2.
Поскольку обычная k-блочная стратегия в данном случае терпит неудачу, вместо нее библиотека scikit-learn предлагает использовать для классификации стратифицированную k-блочную перекрестную проверку (stratified k-fold cross-validation). В стратифицированной перекрестной проверке мы разбиваем данные таким образом, чтобы пропорции классов в каждом блоке в точности соответствовали пропорциям классов в наборе данных
mglearn.plots.plot_stratified_cross_validation()
Перекрёстный контроль со случайными разбиениями
Еще одной, очень гибкой стратегией перекрестной проверки является перекрестная проверка со случайными перестановками при разбиении (shuffle-split cross-validation). В этом виде проверки каждое разбиение выбирает train_size точек для обучающего набора и test_size точек для тестового набора (при этом обучающее и тестовое подмножества не пересекаются). Точки выбираются с возвращением. Разбиение повторяется n_iter раз.
from sklearn.model_selection import ShuffleSplit
shuffle_split = ShuffleSplit(test_size=.5, train_size=.5, n_splits=10)
scores = cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
print("Cross-validation scores:\n{}".format(scores))
Cross-validation scores: [0.97333333 0.98666667 0.94666667 0.94666667 0.94666667 0.94666667 0.98666667 0.97333333 0.93333333 0.97333333]

Поиск по решётке
Простой пример
Рассмотрим применение ядерного метода SVM с ядром RBF (радиальной базисной функцией), реализованного в классе SVC. В ядерном методе опорных векторов есть два важных параметра: ширина ядра gamma и параметр регуляризации C. Допустим, мы хотим попробовать значения 0.001, 0.01, 0.1, 1, 10 и 100 для параметра С и то же самое для параметра gamma. Поскольку нам нужно попробовать шесть различных настроек для C и gamma, получается 36 комбинаций параметров в целом. Все возможные комбинации формируют таблицу (которую еще называют решеткой или сеткой) настроек параметров для SVM.
Теперь можно реализовать простой решетчатый поиск с помощью вложенных циклов for по двум параметрам, обучая и оценивая классификатор для каждой комбинации.
# naive grid search implementation
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=0)
print("Size of training set: {} size of test set: {}".format(
X_train.shape[0], X_test.shape[0]))
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters, train an SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# evaluate the SVC on the test set
score = svm.score(X_test, y_test)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
print("Best score: {:.2f}".format(best_score))
print("Best parameters: {}".format(best_parameters))
Size of training set: 112 size of test set: 38
Best score: 0.97
Best parameters: {'C': 100, 'gamma': 0.001}
Переобучение (ovefitting) и тестовые выборки
Итак, перебрали множество значений параметров и выбрали ту комбинацию значений, которая дает наилучшее качество на тестовом наборе, но это вовсе не означает, что на новых данных мы получим такое же значение функционала качества. Поскольку мы использовали тестовый набор для настройки параметров, мы больше не можем использовать его для оценки качества модели. Это та же самая причина, по которой нам изначально нужно разбивать данные на обучающий и тестовый наборы. Теперь для оценки качества модели нам необходим независимый набор данных, то есть набор, который не использовался для построения модели и настройки ее параметров. Один из способов решения этой проблемы заключается в том, чтобы разбить данные еще раз, таким образом, мы получаем три набора: обучающий набор для построения модели, проверочный (валидационный) набор для выбора параметров модели, а также тестовый набор для оценки качества работы выбранных параметров.

После выбора наилучших параметров с помощью проверочного набора проверки, мы можем заново построить модель, используя найденные настройки, но теперь на основе объединенных обучающих и проверочных данных. Таким образом, мы можем использовать для построения модели максимально возможное количество данных.
from sklearn.svm import SVC
# split data into train+validation set and test set
X_trainval, X_test, y_trainval, y_test = train_test_split(
iris.data, iris.target, random_state=0)
# split train+validation set into training and validation sets
X_train, X_valid, y_train, y_valid = train_test_split(
X_trainval, y_trainval, random_state=1)
print("Size of training set: {} size of validation set: {} size of test set:"
" {}\n".format(X_train.shape[0], X_valid.shape[0], X_test.shape[0]))
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters, train an SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# evaluate the SVC on the validation set
score = svm.score(X_valid, y_valid)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# rebuild a model on the combined training and validation set,
# and evaluate it on the test set
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
test_score = svm.score(X_test, y_test)
print("Best score on validation set: {:.2f}".format(best_score))
print("Best parameters: ", best_parameters)
print("Test set score with best parameters: {:.2f}".format(test_score))
Size of training set: 84 size of validation set: 28 size of test set: 38
Best score on validation set: 0.96
Best parameters: {'C': 10, 'gamma': 0.001}
Test set score with best parameters: 0.92
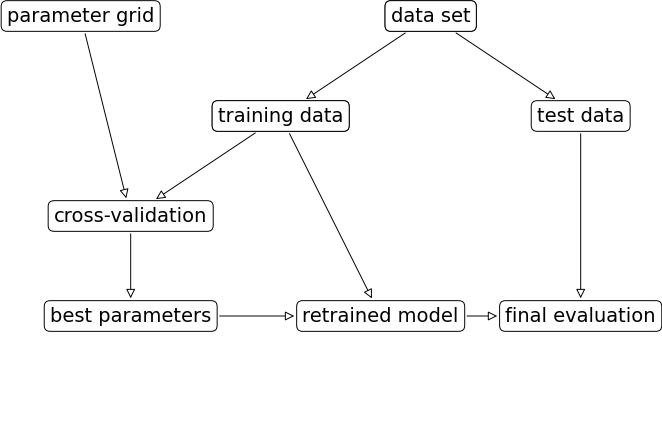
Поиск по решётке с перекрёстной проверкой (Grid search cross-validation)
Хотя только что рассмотренный нами метод разбиения данных на обучающий, проверочный и тестовый наборы является вполне рабочим и относительно широко используемым, он весьма чувствителен к правильности разбиения данных. Взглянув на вывод, приведенный для предыдущего фрагмента программного кода, мы видим, что GridSearchCV 282 выбрал в качестве лучших параметров 'C': 10, 'gamma': 0.001, тогда как вывод, приведенный для программного кода в предыдущем разделе, сообщает нам, что наилучшими параметрами являются 'C': 100, 'gamma': 0.001. Для лучшей оценки обобщающей способности вместо одного разбиения данных на обучающий и проверочный наборы мы можем воспользоваться перекрестной проверкой. Теперь качество модели оценивается для каждой комбинации параметров по всем разбиениям перекрестной проверки.
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters,
# train an SVC
svm = SVC(gamma=gamma, C=C)
# perform cross-validation
scores = cross_val_score(svm, X_trainval, y_trainval, cv=5)
# compute mean cross-validation accuracy
score = np.mean(scores)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# rebuild a model on the combined training and validation set
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
SVC(C=10, gamma=0.1)
Чтобы c помощью пятиблочной перекрестной проверки оценить качество SVM для конкретной комбинации значений C и gamma, нам необходимо обучить 36*5=180 моделей. Как вы понимаете, основным недостатком использования перекрестной проверки является время, которое требуется для обучения всех этих моделей.
Если используется тестовая выборка. то настройка параметров модели будет происходить по следующей схеме.
Функционалы качества (loss functions)
Прежде чем выбрать показатель качества машинного обучения, нужно подумать о высокоуровневой цели вашего проекта, которую часто называют бизнес- метрикой (business metric). Последствия, обусловленные выбором конкретного алгоритма для того или иного проекта, называются влиянием на бизнес (business impact).
Задача с 2 классами. Типы ошибок и их представление, ROC-кривая
В статистике ложно положительный пример известен как ошибка I рода (type I error, пропуск цели), а ложно отрицательный пример – как ошибка II рода (type II error, ложная тревога). Их также называют «ложно отрицательный пример» и «ложно положительный пример».
Одним из наиболее развернутых способов, позволяющих оценить качество бинарной классификации, является использование матрицы ошибок. Давайте исследуем прогнозы модели LogisticRegression, построенной в предыдущем разделе, с помощью функции confusion_matrix. Прогнозы для тестового набора данных мы уже сохранили в pred_logreg
from sklearn.metrics import confusion_matrix
confusion = confusion_matrix(y_test, pred_logreg)
print("Confusion matrix:\n{}".format(confusion))
Confusion matrix: [[402 1] [ 6 41]]
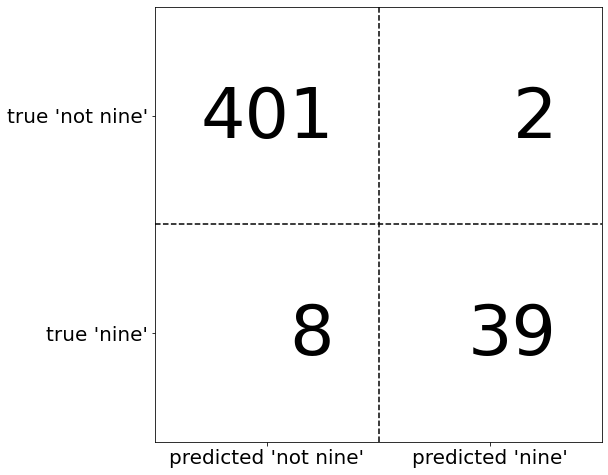

Эмпирический риск (правильность) – это количество верно классифицированных примеров (TP и TN), поделенное на общее количество примеров (суммируем все элементы матрицы ошибок).
Есть еще несколько способов подытожить информацию матрицы ошибок, наиболее часто используемыми из них являются точность и полнота. Точность (precision) показывает, сколько из предсказанных положительных примеров оказались действительно положительными. Таким образом, точность – это доля истинно положительных примеров от общего количества предсказанных положительных примеров.
С другой стороны, полнота (recall) показывает, сколько от общего числа фактических положительных примеров было предсказано как положительный класс. Полнота – это доля истинно положительных примеров от общего количества фактических положительных примеров.
ROC-кривые и рабочие точки
Требование, выдвигаемое к качеству модели (например, значение полноты должно быть 90%), часто называют рабочей точкой (operating point). Фиксирование рабочей точки часто бывает полезно в контексте бизнеса, чтобы гарантировать определенный уровень качества клиентам или другим группам лиц внутри организации. Как правило, при разработке новой модели нет четкого представления о том, что будет рабочей точкой. По этой причине, а также для того, чтобы получить более полное представление о решаемой задаче, полезно сразу взглянуть на все возможные пороговые значения или все возможные соотношения точности и полноты для этих пороговых значений. Данную процедуру можно осуществить с помощью инструмента, называемого кривой точности-полноты (precision-recall curve). Функцию для вычисления кривой точности-полноты можно найти в модуле sklearn.metrics. Ей необходимо передать фактические метки классов и спрогнозированные вероятности, вычисленные с помощью decision_function или predict_proba
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))
# Use more data points for a smoother curve
X, y = make_blobs(n_samples=(4000, 500), cluster_std=[7.0, 2], random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))
# find threshold closest to zero
close_zero = np.argmin(np.abs(thresholds))
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.xlabel("Precision")
plt.ylabel("Recall")
plt.legend(loc="best")
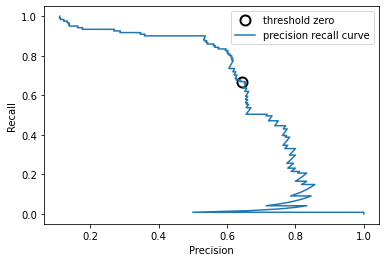
Кривая рабочей характеристики приемника (receiver operating characteristics curve) или кратко ROC-кривая (ROC curve), как и кривая точности-полноты, позволяет рассмотреть все пороговые значения для данного классификатора, но вместо точности и полноты она показывает долю ложно положительных примеров (false positive rate, FPR) в сравнении с долей истинно положительных примеров (true positive rate). Вспомним, что доля истинно положительных примеров – это просто еще одно название полноты, тогда как доля ложно положительных примеров – это доля ложно положительных примеров от общего количества отрицательных примеров. ROC-кривую можно вычислить с помощью функции roc_curve
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test, svc.decision_function(X_test))
plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
# find threshold closest to zero
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
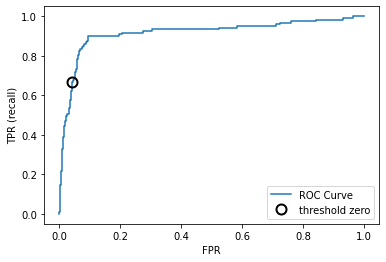
Идеальная ROC-кривая проходит через левый верхний угол, соответствуя классификатору, который дает высокое значение полноты при низкой доле ложно положительных примеров. Проанализировав значения полноты и FPR для порога по умолчанию 0, мы видим, что можем достичь гораздо более высокого значения полноты (около 0.9) лишь при незначительном увеличении FPR. Точка, ближе всего расположенная к верхнему левому углу, возможно, будет лучшей рабочей точкой, чем та, что выбрана по умолчанию. Опять же, имейте в виду, что для выбора порогового значения следовать использовать отдельный проверочный набор, а не тестовые данные.
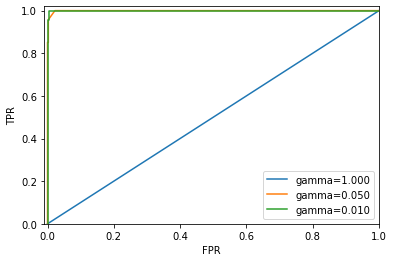
Можно сравнить работу одного алгоритма для разных значений параметров. Например, вернемся к задаче, которую мы решали ранее, классифицируя в наборе digits девятки и остальные цифры. Мы классифицируем наблюдения, используя SVM с тремя различными настройками ширины ядра и gamma.
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)
plt.figure()
for gamma in [1, 0.05, 0.01]:
svc = SVC(gamma=gamma).fit(X_train, y_train)
accuracy = svc.score(X_test, y_test)
auc = roc_auc_score(y_test, svc.decision_function(X_test))
fpr, tpr, _ = roc_curve(y_test , svc.decision_function(X_test))
print("gamma = {:.2f} accuracy = {:.2f} AUC = {:.2f}".format(
gamma, accuracy, auc))
plt.plot(fpr, tpr, label="gamma={:.3f}".format(gamma))
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.xlim(-0.01, 1)
plt.ylim(0, 1.02)
plt.legend(loc="best")
gamma = 1.00 accuracy = 0.90 AUC = 0.50 gamma = 0.05 accuracy = 0.90 AUC = 1.00 gamma = 0.01 accuracy = 0.90 AUC = 1.00