Предобработка данных

Содержание

Эквализация гистограмм.
- Теория
Преобразования Фурье

Эквализация гистограмм.

Код к эквализации notebook

Данные по раку

Гистогра́мма (в фотографии) — это график статистического распределения элементов цифрового изображения с различной яркостью, в котором по горизонтальной оси представлена яркость, а по вертикали — относительное число пикселов с конкретным значением яркости.

В черно-белом изображении яркость непосредственно определяется значением пиксела. Чем больше значение пиксела (чем он светлее) - тем он ярче.

В цветных изображениях, обычно, каждый пиксел описывается тремя параметрами: долей красного в цвете, долей зеленого в цвете, долей синего в цвете. Тогда, для вычисления яркости используется взвешенная сумма каждого из значений пикселов.

Вот примеры гистограмм изображений.

Как мы видим, если изображение сильно цветное, то гистограмма более или менее равномерна.

Если много черного цвета, то "горб" гистограммы ближе к левому краю, если много белого, то к правому.

Эквализация

Рассмотрим задачу эквализации (спрямления) распределения. Т.е. из чисел, которые распределены, например, по такому закону:

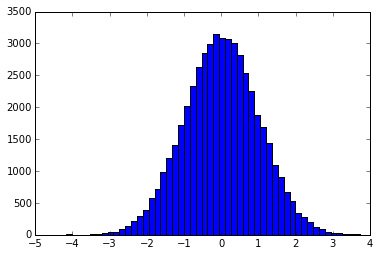
При помощи некоторого правила числа меняются. После изменения данные становятся распределенными по равномерному такому закону:

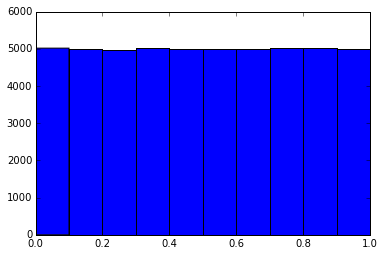
Даная операция применяется в обработке изображений для Увеличения яркости/контрастности и качества изображения вцелом.

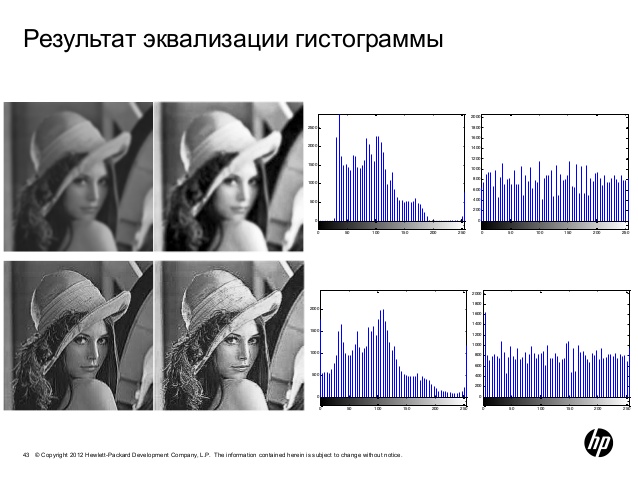
Перцентили

Перцентиль p - это число a, такое, что, если взять из интересующей последовательности A все числа, меньше a, то количество этих чисел будет составлять p% от общей длинны последовательности A.

Другое объяснение, что Перцентиль p - это число а, такое что, если отсортировать исходную последовательность А, то p% чисел окажутся слева от а.

Для вычисления перцентилей в numpy встроенна функция numpy.percentile(values, percentile)'

Рассмотрим пример ее работы:

>>> values = [3, 4, 1, 2, 5, 6, 7, 8, 9, 10]
>>> np.percentile(values, 20)
2.8
>>> np.percentile(values, 40)
4.6

Квантильная нормализация включает в себя три шага:

отсортировать значения по каждому столбцу;
найти среднее каждой результирующей строки;
заменить квантиль каждого столбца на квантиль среднего столбца.

Далее приведём пример использования эквализации гистограмм при работе с данныи экспрессии генов. В качестве примера взяты данные из работы paper

import numpy as np
from scipy import stats

def quantile_norm(X):
    """Normalize the columns of X to each have the same distribution.

    Given an expression matrix (microarray data, read counts, etc) of M genes
    by N samples, quantile normalization ensures all samples have the same
    spread of data (by construction).

    The data across each row are averaged to obtain an average column. Each
    column quantile is replaced with the corresponding quantile of the average
    column.

    Parameters
    ----------
    X : 2D array of float, shape (M, N)
        The input data, with M rows (genes/features) and N columns (samples).

    Returns
    -------
    Xn : 2D array of float, shape (M, N)
        The normalized data.
    """
    # compute the quantiles
    quantiles = np.mean(np.sort(X, axis=0), axis=1)

    # compute the column-wise ranks. Each observation is replaced with its
    # rank in that column: the smallest observation is replaced by 1, the
    # second-smallest by 2, ..., and the largest by M, the number of rows.
    ranks = np.apply_along_axis(stats.rankdata, 0, X)

    # convert ranks to integer indices from 0 to M-1
    rank_indices = ranks.astype(int) - 1

    # index the quantiles for each rank with the ranks matrix
    Xn = quantiles[rank_indices]

    return(Xn)

По причине характера вариабельности, присутствующей в количественных данных экспрессии генов, общепринято перед квантильной нормализацией логарифмически преобразовывать данные. Поэтому мы напишем дополнительную вспомогательную функцию, которая будет выполнять это преобразование:

def quantile_norm_log(X):
    logX = np.log(X + 1)
    logXn = quantile_norm(logX)
    return logXn

Данные по экспрессии генов до эквализации:

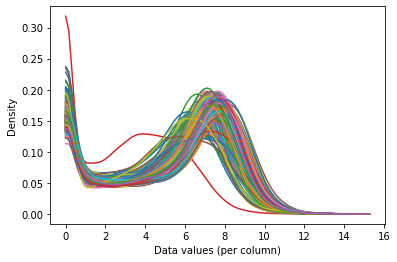
Главный сдвиг в распределении, который мы наблюдаем, говорит о том, что эти различия технические. Иными словами, наличие изменений, скорее всего, вызвано различиями в обработке каждого образца, а не биологической ва- риацией. Поэтому мы попытаемся нормализовать эти глобальные различия между индивидуумами.

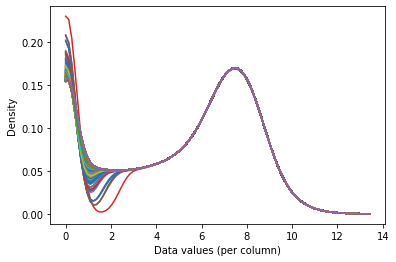
Распределения теперь выглядят почти одинаково - различаются только левые хвосты.

Преобразования Фурье

Код к Фурье Fourier

Введение

ДПФ (дискретное преобразование Фурье ) преобразовывает последовательность из N равномерно расположенных ве щественных или комплексных чисел x₀, x₁, …, x_N − 1 функции x(t) в последовательность из N комплексных чисел X_k :

X_k = ^N − 1∑_n = 0x_ne^{− j2πkn ⁄ N}, k = 0, 1, …, N − 1.

Если числа Xk известны, то обратное Фурье-преобразование восстанавливает выборочные значения xn единственным способом. т.е. ДФТ полностью обратимо:

x_n = (1)/(N)^N − 1∑_k = 0X_ke^{j2πkn ⁄ N}

Если исходная функция x(t) будет ограничиваться по частоте менее половиной час тоты дискретизации (так называемой частотой Найквиста- Котельникова), то интерполяция между выборочными значениями, производимая обратным ДПФ-преобразованием, обычно будет давать верную реконструкцию x(t) (теорема Шеннона-Котельникова). Если x(t) как таковая не ограничивается, то обратное ДПФ-преобразование не может в целом путем интерполяции использоваться для реконструкции x(t). Обратите внимание, данное ограничение не подразумевает от- сутствия методов, позволяющих выполнять такую реконструкцию. Возьмем, например, методы восстановления сигнала с использованием знаний о его предыдущих разрежен- ных или сжатых значениях (compressed sensing) или методы выборки сигналов с конеч- ной интенсивностью обновления (FRI-сигналов).

Функция e^{j2πk ⁄ N} = (e^{j2π ⁄ N})^k = w^k принимает дискретные значения между 0 и на еди- ничном круге в комплексной плоскости. Функция e^{j2πkn ⁄ N} = w^kn обходит начало координат n(N − 1)/(N) раз, в результате генерируя гармонику , для которой n = 1 .

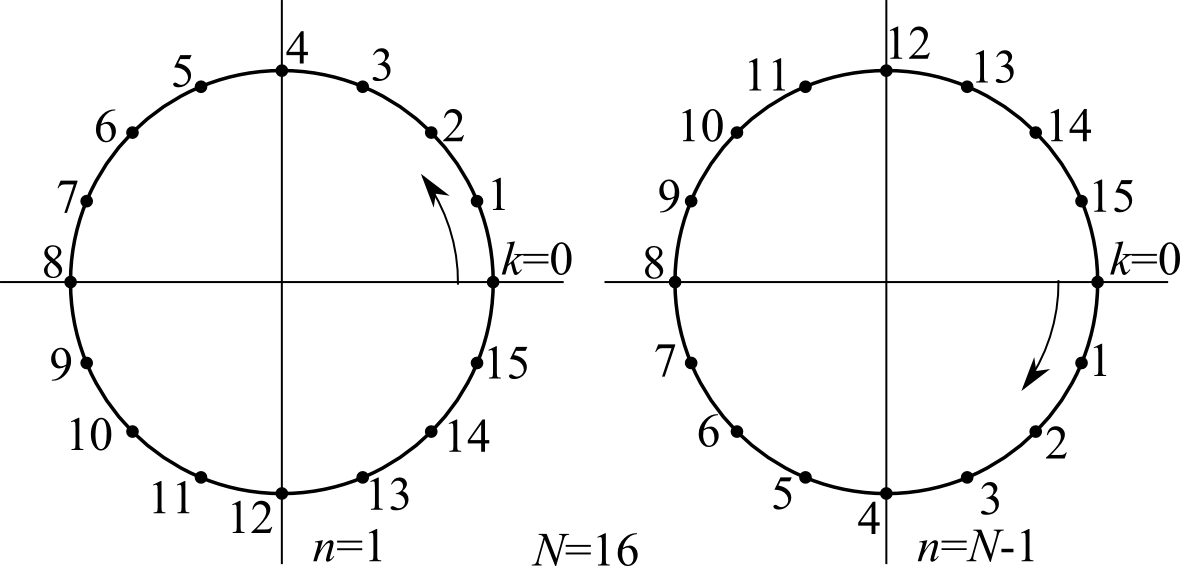
Unit circle samples

Быстрое преобразование Фурье (fft), в свою очередь, просто является специальным и очень эффективным алгоритмом вычисления ДПФ. В отличие от прямого вычисления ДПФ, занимающего порядка N² вычислений, алгоритм БПФ занимает порядка NlogN вычислений. БПФ стал ключевым в широком распространении ДПФ в приложениях, работающих в режиме реального времени, и в 2000 г. журналом IEEE Computing Science & Engineering он был включен в список лучших 10 алгоритмов XX века.

Реализации

Функционал ДПФ библиотеки SciPy расположен в модуле scipy.fftpack.

fft, fft2, fftn: быстрое преобразование Фурье соответственно 1, 2, или n мерных массивов.
ifft, ifft2, ifftn: обратное быстрое преобразование Фурье
dct, idct, dst, idst: синусное и косинусное преобразования.
fftshift, ifftshift: преобразования с задаваемым значением нулевой частоты.
fftfreq: возвращает также вектор частот.
rfft: действительный аналог fft - используется по умолчанию для действительных векторов.

Для оконных свёртк используются функции NumPy:

np.hanning, np.hamming, np.bartlett, np.blackman, np.kaiser

или же - scipy.signal.fftconvolve .

Пример. Подавление шума

Рассмотрим изображение

Для исследования спектра, поскольку изображение имеет более одной раз- мерности, чтобы вычислить ДПФ, применим вместо функции fft функцию fftn. Двумерное БПФ-преобразование эквивалентно взятию одномерного БПФ в строках и затем в столбцах, или наоборот.

F = fftpack.fftn(image)

F_magnitude = np.abs(F)
F_magnitude = fftpack.fftshift(F_magnitude)

Далее, посчитаем логарифм спектра

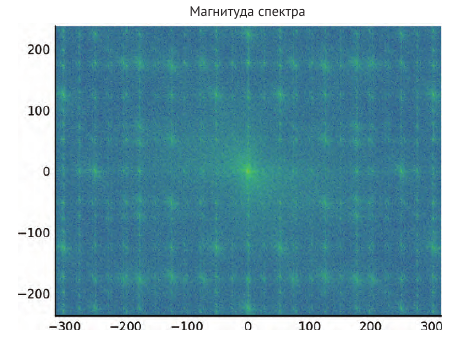
f, ax = plt.subplots(figsize=(4.8, 4.8))

ax.imshow(np.log(1 + F_magnitude), cmap='viridis',
          extent=(-N // 2, N // 2, -M // 2, M // 2))
ax.set_title('Spectrum magnitude');

Обратите внимание на высокие значения вокруг источника (середины) спектра. Эти коэффициенты описывают низкие частоты или сглаживают части изображения, размывшие полотно фотографии. Более высокочастотные ком- поненты, распространенные по всему спектру, заполняют края и детализацию. Пики вокруг более высоких частот соответствуют периодическому шуму. Из фотографии мы видим, что шум (артефакты измерения) имеет высоко- периодический характер. Поэтому попробуем удалить его, обнулив соответ- ствующие части спектра.

# Set block around center of spectrum to zero
K = 40
F_magnitude[M // 2 - K: M // 2 + K, N // 2 - K: N // 2 + K] = 0

# Find all peaks higher than the 98th percentile
peaks = F_magnitude < np.percentile(F_magnitude, 98)

# Shift the peaks back to align with the original spectrum
peaks = fftpack.ifftshift(peaks)

# Make a copy of the original (complex) spectrum
F_dim = F.copy()

# Set those peak coefficients to zero
F_dim = F_dim * peaks.astype(int)

# Do the inverse Fourier transform to get back to an image
# Since we started with a real image, we only look at the real part of
# the output.
image_filtered = np.real(fftpack.ifft2(F_dim))

f, (ax0, ax1) = plt.subplots(2, 1, figsize=(4.8, 7))
ax0.imshow(fftpack.fftshift(np.log10(1 + np.abs(F_dim))), cmap='viridis')
ax0.set_title('Spectrum after suppression')

ax1.imshow(image_filtered)
ax1.set_title('Reconstructed image');

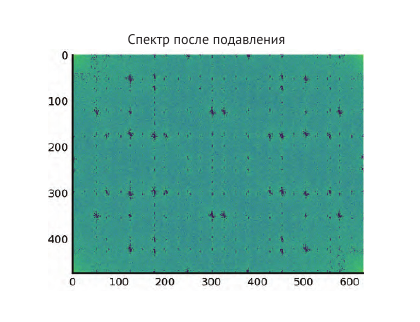
Оконные преобразования

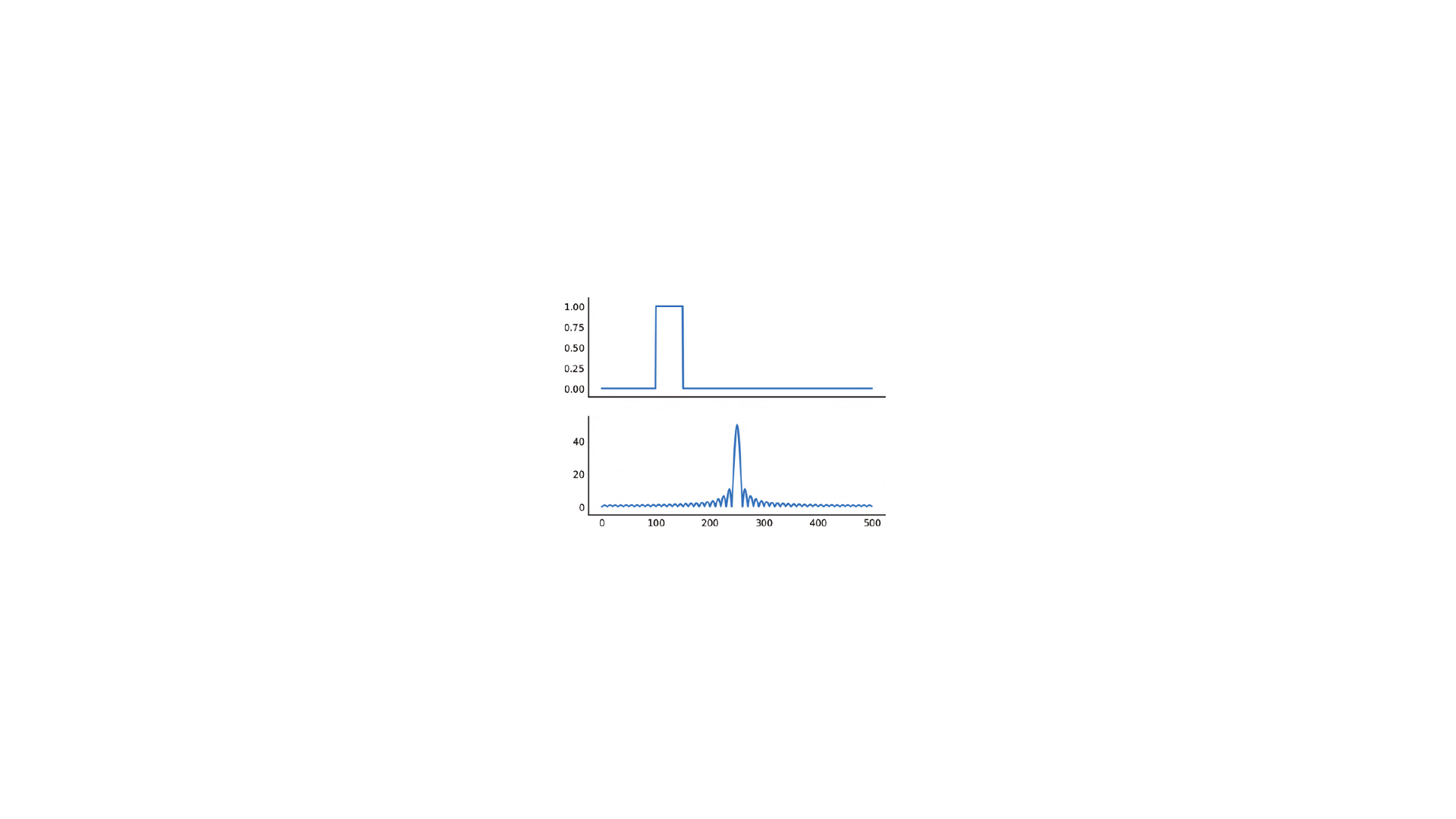
Если исследовать преобразование Фурье прямоугольного импульса, то мы уви- дим значительные боковые лепестки в спектре:

x = np.zeros(500)
x[100:150] = 1

X = fftpack.fft(x)

f, (ax0, ax1) = plt.subplots(2, 1, sharex=True)

ax0.plot(x)
ax0.set_ylim(-0.1, 1.1)

ax1.plot(fftpack.fftshift(np.abs(X)))
ax1.set_ylim(-5, 55);

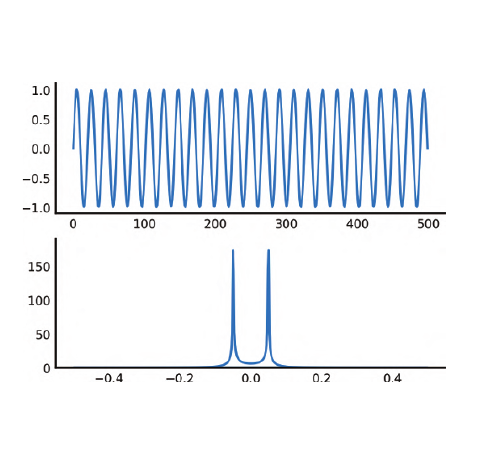
Аналогично, для любого конечного сигнала увидим всегда сглаженный спектр. Например, для 1 синусоиды.

t = np.linspace(0, 1, 500)
x = np.sin(49 * np.pi * t)

X = fftpack.fft(x)

f, (ax0, ax1) = plt.subplots(2, 1)

ax0.plot(x)
ax0.set_ylim(-1.1, 1.1)

ax1.plot(fftpack.fftfreq(len(t)), np.abs(X))
ax1.set_ylim(0, 190);

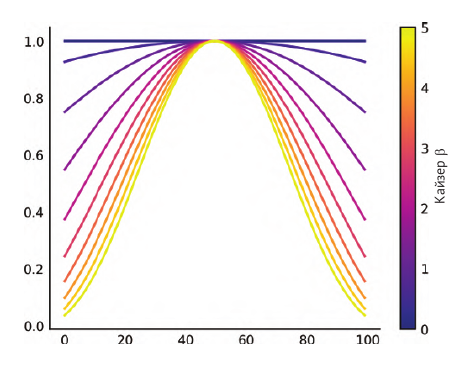
Этот эффект можно купировать оконным преобразованием. Ниже приведено кайзеровское окно для разных хначений параметра K(N, β), β от 0 до 100:

f, ax = plt.subplots()

N = 10
beta_max = 5
colormap = plt.cm.plasma

norm = plt.Normalize(vmin=0, vmax=beta_max)

lines = [
    ax.plot(np.kaiser(100, beta), color=colormap(norm(beta)))
    for beta in np.linspace(0, beta_max, N)
    ]

sm = plt.cm.ScalarMappable(cmap=colormap, norm=norm)

sm._A = []

plt.colorbar(sm).set_label(r'Kaiser $\beta$');

С применением окна пример с синусоидой будет выглядеть так

win = np.kaiser(len(t), 5)
x_win = x * win

X_win = fftpack.fft(x_win)

f, (ax0, ax1) = plt.subplots(2, 1)

ax0.plot(x_win)
ax0.set_ylim(-1.1, 1.1)

ax1.plot(fftpack.fftfreq(len(t)), np.abs(X_win))
ax1.set_ylim(0, 190);