Scikit-learn : основные структуры
Содержание
- Задание (на это и следующее занятие):
- Код к семинару
- Представление данных
- API оценивающих функций (estimators)
- Как пользоваться sklearn API
- Обучение с учителем: Линейная регрессия
- Классификация: наивный байесов классификатор
- Обучение без учителя: размерность набора данных про ирисы
- Обучение без учителя: кластеризация
- Загрузка и визуализация
- Снижение размерности
- Классификация
- Выводы
- This notebook contains an excerpt from the
by Jake VanderPlas; the content is available
Код к семинару
Крайне полезная ссылка про то, с чего начинать при работе с набором данных data exploration
Введение в Scikit-Learn
Scikit-Learn - один из очень многих модулей, предоставляющих реализации моделей и алгоритмов машинного обучения, пожалуй, наиболее полный и эффективный. Отличается ясным , унифицированным и чень подробно документированным API.
Попытаемся рассмотреть основыне принципы интерфейса и способов организации данных и подходы к реализаци алгоритмов.
Как обычно, сперва рассмотрим Модель представления данных и интерфейс оценивающих функций (estimators) , а потом рассмотрим на примерах, как эти структуры работают.
Представление данных
Машинное обучение занимается построением моделей из данных. Поэтому перво-наперво надо понять, как данные представляются внутри sklearn. Это можно сформулировать одним главным принципом:
набор данных = таблица (dataframe)
В этой таблице всегда + строки = прецеденты (samples) + столбцы = признаки (features, attributes)
Пример с любимыми ирисами Фишера Iris dataset ,
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', size=1.5);
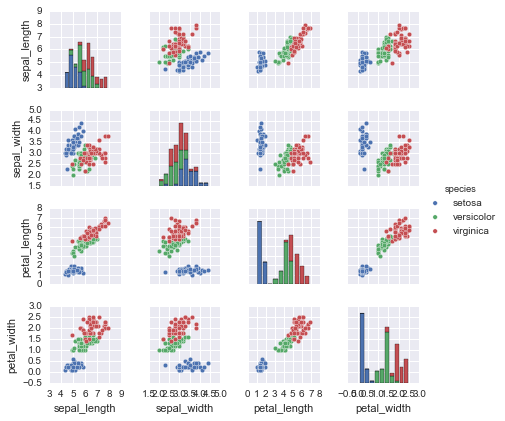
Для использования в Scikit-Learn, нужно из DataFrame сформировать отдельно признаковую матрицу и вектор ответов:
X_iris = iris.drop('species', axis=1)
X_iris.shape
(150, 4)
y_iris = iris['species']
y_iris.shape
(150,)
Схематично это можно изобразить так:
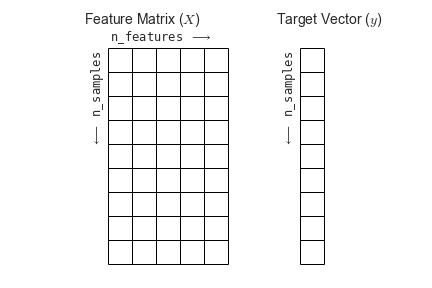
API оценивающих функций (estimators)
Основные принципы интерфейса sklearn были в своё время сформулированы в статье Scikit-Learn API paper :
- Согласованность: У всех классов используется унифицированный набор стандартных методов (функций), полностью описанных в документации.
- Проверяемость: Все важные параметры алгоритмов задаются как обычные аргументами.
- Простая иерархия: Только алгоритмы реализованы классами, для наборов данных используются более простые стандартные типы других библиотек (NumPy arrays, Pandas DataFrames, SciPy sparse matrices) , названия признаков - обычные строки.
- Композиция: Более сложные задачи можно решить с помощью композиций базовых алгоритмов.
- Разумные умолчания: Если есть параметры, которые долны быть заданы пользователем, - всегда есть обоснованные значения по умолчанию.
Следование этим принципам существенно унифицирует форму представления методов анализа данных и упрощает освоение/реализацию новых алгоритмов и использование уже существующих.
Как пользоваться sklearn API
Как правило, работа с sklearn строится следующим образом
- Выбрать класс моделей для работы с данными, заимпортить соответствующий подкласс Scikit-Learn.
- Фиксировать значения гиперпараметров модели и инстанцировать выбранный класс с этими значениями атрибутов.
- Представить данные в виде признаковой матрицы и вектора ответов как описано выше.
- Обучить модель на данных, вызвав метод fit() .
- Применить полученную модель к новым порциям данных:
- для обучения с учителем используется метод predict() .
- дя обучения без учителя применяется transform() для отображений или тот же predict() для новых прецедентов.
Разберём это на примерах.
Обучение с учителем: Линейная регрессия
Один из самых простых примеров - приближение данных вида (x, y) линейной функцией :
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(42)
x = 10 * rng.rand(50)
y = 2 * x - 1 + rng.randn(50)
plt.scatter(x, y);
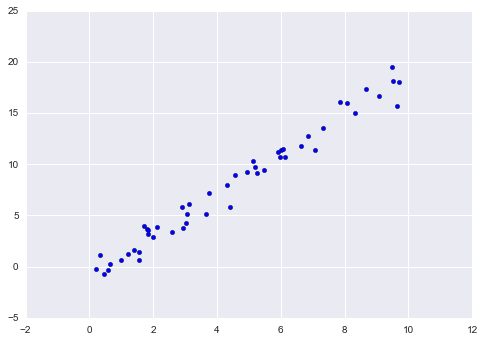
Последовательно, по этапам:
- Выбор класса моделей
В Scikit-Learn, класс моделей всегда соответствует классу в смысле ООП. То есть, в случае с линейной регрессией надо использовать соответствующи одноимённый класс:
from sklearn.linear_model import LinearRegression
Разумеется, в sklearn.linear_model есть и более сложные регрессионные модели .
- Гиперпараметры
Разумеется, класс моделей не есть конкретная модель.
Как только фиксирован класс моделей - те не менее остаются некоторые степени свободы. В зависимости от выбранного класса моделей, прежде обучения, придётся ответить на вопросы типа следующих:
- нужен ли сдвиг относительно начала координат?
- нужна ли нормализация?
- нужна ли предобработка признаков. чтоб модель была более гибкой?
- нужна ли регуляризация?
- сколько компонент надо использовать?
Ответ на перечисленные вопросы и некоторые другие формируется в виде выбора гиперпараметров, или скрытых параметров модели. В Scikit-Learn, они задаются как параметры создаваемого (т.е инстанцируемого) объекта.
Итак, инстанцируется класс LinearRegression , подстраиваемся под сдвиг от начала координат с помощью параметра fit_intercept :
model = LinearRegression(fit_intercept=True)
model
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
После инстанцирования создан экземпляр алгоритма в выбранной модели. Теперь можно с ним работать: в Scikit-Learn API понятия выбора модели и применения модели к данным.
- Стандартизация данных
Пусть ранее мы представили входные данные в стандартном виде признаковая матрица + вектор ответов:
X = x[:, np.newaxis]
X.shape
(50, 1)
- Обучение
Теперь можно собственно обучить модель на данных. По сути это в большинстве случев означает оптимизацию модели по внутренним параметрам. Это делается с помощью метода fit() :
model.fit(X, y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Теперь внутрение параметры модели приведены к некоторому оптимальному значению, и пользователь может их увидеть. По традиции, все внутренние параметры, настраиваемые с помощью fit() имеют подчёркивание в конце:
model.coef_
array([ 1.9776566])
model.intercept_
-0.90331072553111635
Эти два параметра представляют собой угловой коэффициент и точку пересе- чения с осью координат для простой линейной аппроксимации наших данных. Сравнивая с описанием данных, видим, что они очень близки к исходному угловому коэффициенту, равному 2, и точке пересечения, равной –1.
Часто возникает вопрос относительно погрешностей в подобных внутрен- них параметрах модели. В целом библиотека Scikit-Learn не предоставляет инструментов, позволяющих делать выводы непосредственно из внутренних параметров модели: интерпретация параметров скорее вопрос статистического моделирования, а не машинного обучения. Машинное обучение концентрируется в основном на том, что предсказывает модель. Для тех, кто хочет узнать больше о смысле подбираемых параметров модели, существуют другие инструменты, включая пакет Statsmodels Python package .
- Апробация на новых данных
После обучения модели главная задача машинного обучения с учителем заклю- чается в вычислении с ее помощью значений для новых данных, не являющихся частью обучающей последовательности. Сделать это в библиотеке Scikit-Learn можно посредством метода predict() .
xfit = np.linspace(-1, 11)
Как обычно, надо скомпоновать прецеденты в признаковую матрицу размера [n_samples, n_features] :
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
Теперь, отрисуем то, что получилось: данные и полученную модель:
plt.scatter(x, y)
plt.plot(xfit, yfit);
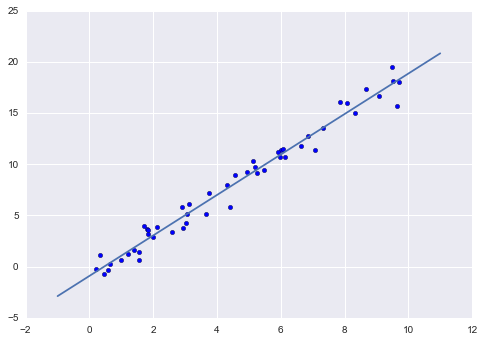
Обычно эффективность модели оценивают, сравнивая ее результаты с эталоном, как мы увидим в следующем примере.
Классификация: наивный байесов классификатор
Насколько хорошо мы сможем предсказать метки остальных данных с помощью модели, обученной на некоторой части данных набора Iris? Для этой задачи мы воспользуемся чрезвычайно простой обобщенной моделью, из- вестной под названием «Гауссов наивный байесовский классификатор» (он же дискриминант Фишера ),
исходящей из допущения, что все классы взяты из выровненного по осям координат Гауссова распределения. Гауссов наивный байесовский классификатор в силу отсутствия гипер- параметров и высокой производительности — хороший кандидат на роль эталонной классификации. Имеет смысл поэкспериментировать с ним, прежде чем выяснять, можно ли получить лучшие результаты с помощью более сложных моделей. Мы собираемся проверить работу модели на неизвестных ей данных, так что необходимо разделить данные на обучающую последовательность (training set) и контрольную последовательность (testing set). Это можно сделать вручную, но удобнее воспользоваться вспомогательной функцией train_test_split :
from sklearn.cross_validation import train_test_split
Xtrain, Xtest, ytrain, ytest = train_test_split(X_iris, y_iris,
random_state=1)
После реорганизации данных:
from sklearn.naive_bayes import GaussianNB # 1. choose model class
model = GaussianNB() # 2. instantiate model
model.fit(Xtrain, ytrain) # 3. fit model to data
y_model = model.predict(Xtest) # 4. predict on new data
Теперь с помощью accuracy_score можно узнать долю совпавших ответов:
from sklearn.metrics import accuracy_score
accuracy_score(ytest, y_model)
0.97368421052631582
Как видим, точность превышает 97 %, поэтому для этого конкретного набора дан- ных даже очень наивный алгоритм классификации оказывается эффективным!
Обучение без учителя: размерность набора данных про ирисы
В качестве примера задачи обучения без учителя рассмотрим задачу понижения раз- мерности набора данных Iris с целью упрощения его визуализации. Напомню, что данные Iris четырехмерны: для каждой выборки зафиксированы четыре признака.
В этом разделе мы будем использовать метод главных компонент (PCA).
from sklearn.decomposition import PCA # 1. Choose the model class
model = PCA(n_components=2) # 2. Instantiate the model with hyperparameters
model.fit(X_iris) # 3. Fit to data. Notice y is not specified!
X_2D = model.transform(X_iris) # 4. Transform the data to two dimensions
Построим график полученных результатов. Сделать это быстрее всего можно, вста- вив результаты в исходный объект DataFrame Iris и воспользовавшись функцией lmplot для отображения результатов :
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);
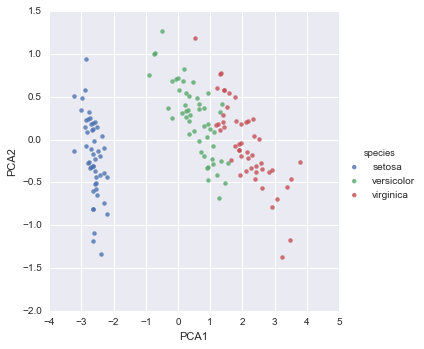
В двумерном представлении виды цветов четко разделены, хотя алгоритм PCA ничего не знает о метках видов цветов.
Обучение без учителя: кластеризация
Теперь рассмотрим кластеризацию набора данных Iris. Алгоритм кластеризации пытается выделить группы данных безотносительно к каким-либо меткам. Здесь мы собираемся использовать мощный алгоритм кластеризации под названием смесь Гауссовых распределений (Gaussian mixture model, GMM)
Метод GMM состоит в попытке моделирования данных в виде набора Гауссовых пятен.
from sklearn.mixture import GMM # 1. Choose the model class
model = GMM(n_components=3,
covariance_type='full') # 2. Instantiate the model with hyperparameters
model.fit(X_iris) # 3. Fit to data. Notice y is not specified!
y_gmm = model.predict(X_iris) # 4. Determine cluster labels
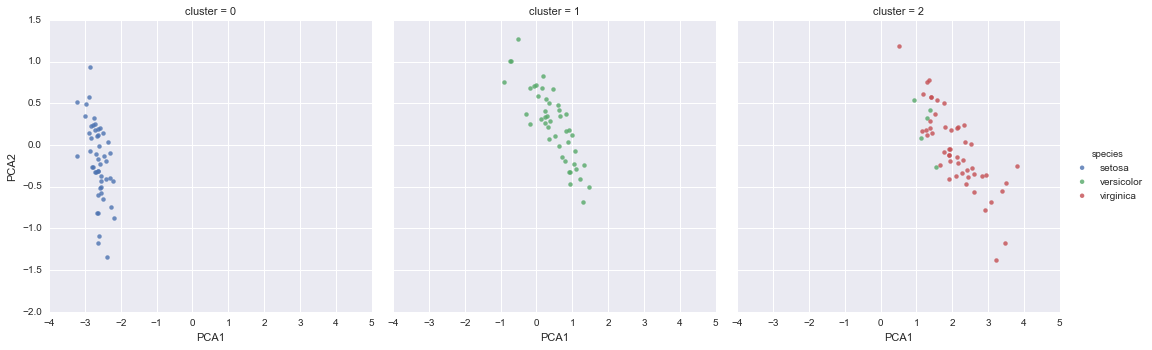
Как и ранее, добавим столбец cluster в DataFrame Iris и воспользуемся библиотекой Seaborn для построения графика результатов:
iris['cluster'] = y_gmm
sns.lmplot("PCA1", "PCA2", data=iris, hue='species',
col='cluster', fit_reg=False);
Более жизненный пример: распознавание цифр
Традиционно эта задача включает как определение местоположения на рисун- ке, так и распознание символов. Мы пойдем самым коротким путем и воспользуемся встроенным в библиотеку Scikit-Learn набором преформатированных цифр.
Загрузка и визуализация
We’ll use Scikit-Learn’s data access interface and take a look at this data:
from sklearn.datasets import load_digits
digits = load_digits()
digits.images.shape
(1797, 8, 8)
Трехмерный массив: 1797 выборок, каждая состоит из сетки пикселов размером 8 × 8. Визуализируем первую их сотню:
import matplotlib.pyplot as plt
fig, axes = plt.subplots(10, 10, figsize=(8, 8),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(digits.images[i], cmap='binary', interpolation='nearest')
ax.text(0.05, 0.05, str(digits.target[i]),
transform=ax.transAxes, color='green')

Для работы с этими данными в библиотеке Scikit-Learn нам нужно получить их двумерное [n_samples, n_features] представление. Для этого мы будем тракто- вать каждый пиксел в изображении как признак, то есть «расплющим» массивы пикселов так, чтобы каждую цифру представлял массив пикселов длиной 64 эле- мента. Кроме этого, нам понадобится целевой массив, задающий для каждой ци- фры предопределенную метку. Эти два параметра встроены в набор данных цифр в виде атрибутов data и target , соответственно:
X = digits.data
X.shape
(1797, 64)
y = digits.target
y.shape
(1797,)
Итого получаем 1797 выборок и 64 признака.
Снижение размерности
Хотелось бы визуализировать наши точки в 64-мерном параметрическом про- странстве, но эффективно визуализировать точки в пространстве такой высо- кой размерности непросто. Понизим вместо этого количество измерений до 2, с помощью метода обучения многообразий Isomap
from sklearn.manifold import Isomap
iso = Isomap(n_components=2)
iso.fit(digits.data)
data_projected = iso.transform(digits.data)
data_projected.shape
(1797, 2)
Теперь наши данные стали двумерными. Построим график этих данных, чтобы увидеть, можно ли что-то понять из их структуры:
plt.scatter(data_projected[:, 0], data_projected[:, 1], c=digits.target,
edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('spectral', 10))
plt.colorbar(label='digit label', ticks=range(10))
plt.clim(-0.5, 9.5);
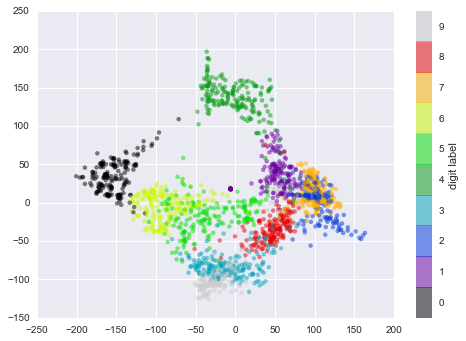
Этот график дает нам представление о разделении различных цифр в 64-мер- ном пространстве. Например, нули (отображаемые черным цветом) и единицы (отображаемые фиолетовым) практически не пересекаются в параметрическом пространстве. На интуитивном уровне это представляется вполне логичным: нули содержат пустое место в середине изображения, а у единиц там, наоборот, черни- ла. С другой стороны, единицы и четверки на графике располагаются сплошным спектром, что понятно, ведь некоторые люди рисуют единицы со «шляпками», из-за чего они становятся похожи на четвёрки.
Различные группы достаточно хорошо разнесены в параметрическом пространстве. Это значит, что даже довольно простой алгоритм классификации с учителем должен работать на них достаточно хорошо.
Классификация
Применим алгоритм классификации к нашим цифрам. Как и в случае с набором данных Iris, разобьем данные на обучающую и контрольную последовательно- сти, после чего обучим на первой из них Гауссову наивную байесовскую модель таким образом:
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, random_state=0)
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(Xtrain, ytrain)
y_model = model.predict(Xtest)
Теперь оценим точность:
from sklearn.metrics import accuracy_score
accuracy_score(ytest, y_model)
0.83333333333333337
Даже при такой исключительно простой модели мы получили более чем 80%-ную точность классификации цифр! Однако из одного числа сложно понять, где наша модель ошиблась. Для этой цели удобна так называемаяматрица различий (confusion matrix), вычислить которую можно спомощью библиотеки Scikit-Learn, а нарисовать посредством Seaborn :
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest, y_model)
sns.heatmap(mat, square=True, annot=True, cbar=False)
plt.xlabel('predicted value')
plt.ylabel('true value');
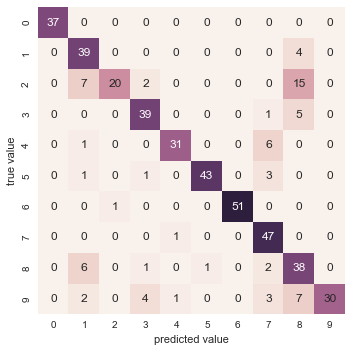
Значительное количество двоек ошибочно классифици - рованы как единицы или восьмерки. Другой способ получения информации о характеристиках модели — построить график входных данных еще раз вместе с предсказанными метками. Мы будем использовать зеленый цвет для правильных меток, и красный — для ошибочных.
fig, axes = plt.subplots(10, 10, figsize=(8, 8),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
test_images = Xtest.reshape(-1, 8, 8)
for i, ax in enumerate(axes.flat):
ax.imshow(test_images[i], cmap='binary', interpolation='nearest')
ax.text(0.05, 0.05, str(y_model[i]),
transform=ax.transAxes,
color='green' if (ytest[i] == y_model[i]) else 'red')

Чтобы поднять нашу точность выше 80 %, можно воспользоваться более сложным алгоритмом, таким как метод опорных векторов ,
или другим методом классификации.
Выводы
В этом разделе мы рассмотрели основные возможности представления данных библиотеки Scikit-Learn, а также API статистического оценивания. Независимо от типа оценивателя применяется одна и та же схема: импорт/создание экземпляра/ обучение/предсказание. Вооружившись этой информацией по API статистического оценивания, вы можете, изучив документацию библиотеки Scikit-Learn, начать экспериментировать, используя различные модели для своих данных.
